Перевод алгебраической формы комплексного числа в тригонометрическую

Переход от алгебраической формы к тригонометрической и показательной

Для того чтобы осуществить переход от алгебраической формы к тригонометрической и показательной, будем использовать следующий алгоритм:

1. Выделить параметры а и b в алгебраической форме .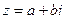

2. Найти модуль комплексного числа r по формуле: .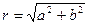

3. Для нахождения аргумента φ выполнить вспомогательный чертеж и определить четверть, в которой расположен вектор 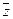(а, следовательно, и угол φ).

4. В зависимости от четверти, в которой лежит угол φ, воспользоваться одной из следующих формул:

Если четверти, то ;

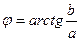
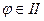
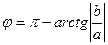
если четверти, то ;

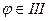
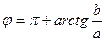
если четверти, то ;

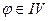
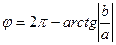
если четверти, то .

5. Подставить найденные значения r и φ в тригонометрическую и показательную формы.

Пример 44.3.Перевести комплексное число 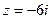в показательную и тригонометрическую формы.

Решение. 1. Выделим параметры а и b в алгебраической форме : , .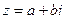

2. Найдем модуль комплексного числа r по формуле : .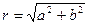

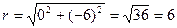
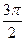
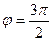
3. Для нахождения аргумента φ выполним вспомогательный чертеж (рис. 44.1). Видим, что полученный вектор образует с положительным направлением оси Ох угол , следовательно, без применения дополнительных формул делаем вывод, что .

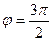
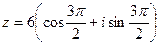
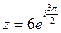
4. Так как r = 6, а , то тригонометрическая форма комплексного числа имеет вид: . Показательная форма того же числа равна .

Ответ: , .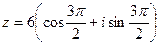

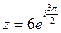
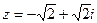
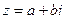
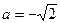
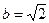
Пример 44.4.Перевести комплексное число в показательную и тригонометрическую формы.

Решение. 1. Выделим параметры а и b в алгебраической форме : , .

2. Найдем модуль комплексного числа r по формуле : .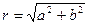

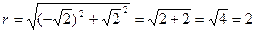
3. Для нахождения аргумента φ выполним вспомогательный чертеж (рис. 44.2). Видим, что полученный вектор (а, следовательно, и угол φ) расположен во второй четверти.

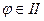
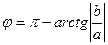
4. Воспользуемся формулой: если четверти, то .

Тогда = = = .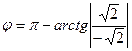

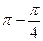
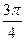
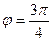
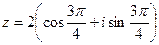
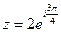
5. Так как r = 2, а , то тригонометрическая форма комплексного числа имеет вид: . Показательная форма того же числа равна .

Ответ: , .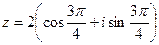

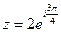
Контрольные вопросы:

1. Каким образом осуществляется переход от тригонометрической формы к алгебраической и показательной?

2. Каким образом осуществляется переход от показательной формы к алгебраической и тригонометрической?

3. Приведите формулы для нахождения модуля и аргумента комплексного числа.

4. Каким образом осуществляется переход от алгебраической формы к показательной и тригонометрической?

РАЗДЕЛ 6. ЧИСЛЕННЫЕ МЕТОДЫ

Численные методы в настоящее время относятся к основным методам решения задач математики и различных ее приложений. Они характеризуются тем, что сводят процесс решения математической задачи к некоторой конечной последовательности операций над числами и приводят к результатам, представленным в виде чисел, матриц, числовых таблиц. Их значение возрастает параллельно с развитием вычислительной техники.

Дата добавления: 2014-12-27 ; Просмотров: 7067 ; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Калькулятор комплексных чисел. Вычисление выражений с комплексными числами

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Калькулятор комплексных чисел

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

Комплексные числа

Комплексные числа — это числа вида x+iy , где x , y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i 2 = -1 ).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi 2 = (ac — bd) + (bc + ad)i
• деление:

Примеры

Найти сумму чисел 5+7i и 5.5-2i :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: 5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: 12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: 2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: 75-50i / (3+4i) = 1 — 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a 2 + b 2 )
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: e z = e a ·cos(b) + i·e a ·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4 2 + (-3) 2 ) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy , где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ) , где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·e iφ , где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

• Найдём радиус (модуль) комплексного числа r: r = √(1 2 + 1 2 ) = √2
• Найдём аргумент числа: φ = arctan(

Источник

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

Подставляя (2) в (1), получим:

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

.

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ. .

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z₁z₂|=r₁r₂, или

т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей .

т.е. аргумент произведения комплексных чисел равен сумме аргументов сомножителей .

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

Отсюда следует, что или

Далее , или

Следовательно, модуль частного двух комплексных чисел равен модулю делимого, деленному на модуль делителя, а аргумент частного двух комплексных чисел получается вычитанием аргумента делителя от аргумента делимого .

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ. .

Источник