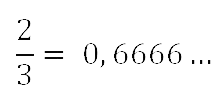Перевод бесконечной десятичной периодической дроби в обыкновенную дробь

Периодическая дробь

Не все обыкновенные дроби можно представить в виде конечной десятичной дроби.

Например, если делить 2 на 3 , то сначала получим ноль целых, потом шесть десятых, а затем при делении всё время будет повторяться остаток 2 , а в частном — цифра 6 .

Такое деление закончить без остатка невозможно и поэтому дробь

нельзя представить в виде конечной десятичной дроби.

Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.

В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.

Вместо 0,666… пишут 0,(6) и читают «ноль целых и шесть в периоде».

Перевод периодической дроби в обыкновенную

Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь.

Рассмотрим периодическую дробь 10,0219(37)

• Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву « k ». У нас « k = 2 ».
• Считаем количество цифр, стоящих после запятой, но до периода десятичной дроби. Обозначаем количество цифр за букву m . У нас « m = 4 ».
• Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа.

Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначаем полученное число буквой « a ».
a = 021937 = 21 937

Подставляем найденные значения в формулу, где « Y » — целая часть бесконечной периодической дроби. У нас « Y = 10 ».

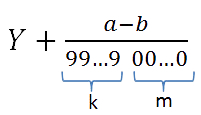
Итак, подставляем все найденные значения в формулу выше и получаем обыкновенную дробь. Полученный ответ всегда можно проверить на обычном калькуляторе.

Источник

Урок по математике «Перевод бесконечной периодической десятичной дроби в обыкновенную дробь»

Краткосрочный план урока по математике

Школа: ГУ«Школа-лицей №1 отдела образования акимата города Костаная»

ФИО учителя: Ермакова Татьяна Александровна

Класс : 6 «____» класс.

Количество присутствующих : отсутствующих :

Перевод бесконечной периодической десятичной дроби в обыкновенную дробь.

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):

6.1.2.21 переводить бесконечную периодическую десятичную дробь в обыкновенную дробь;

Научить записывать бесконечную десятичную периодическую дробь в виде обыкновенной дроби.

переводит бесконечную периодическую десятичную дробь в обыкновенную дробь;

Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.

На данном уроке учащиеся не используют ИКТ

Рациональное число, деление рациональных чисел.

Запланированная деятельность на уроке

Включение в деловой ритм. Организует внимание, готовность к уроку.

Подготовка класса к работе. Слушают, настраиваются на работу

Чтобы разделить два числа с разными знаками, надо:
1) модуль делимого разделить на модуль делителя;
2) перед полученным частным поставить знак « – »
Чтобы разделить два числа с одинаковыми знаками, надо:
1) модуль делимого разделить на модуль делителя;
2) перед полученным частным поставить знак « + »

Периодические дроби делятся на чистые и смешанные, и они подчиняются разным алгоритмам перевода. Сам период представляет собой цифру или группу цифр, неизменно повторяющихся бесконечное количество раз в дробной части. У чистых периодических дробей период расположен сразу после запятой. Для них перевод в обыкновенную дробь заключается в том, что период записывается в числитель, а знаменатель состоит из количества цифр 9, равного количеству цифр в периоде. Пример:

В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом. Пример:

Задание

Обратить в обыкновенные дроби числа:

1) 0,41 (6). В числителе обыкновенной дроби запишем разность между всем числом после запятой (416) и числом после запятой до периода дроби (41). В периоде одна цифра, а после запятой до периода две цифры, поэтому знаменатель будет состоять из одной девятки и двух нулей (900). Итак,

Следующие задания выполняем аналогично.

6)

7)

8)

9)

10)

11)

— О чем говорили на уроке?

— Что удалось без особых усилий?

Вы сегодня хорошо потрудились. Запишите домашнее задание:

Стр 142 № 649 выучить правила

* Стр 142 № 649(1,2) (Необходимо перевести бесконечную периодическую десятичную дробь в обыкновенную дробь)

Источник

Бесконечные периодические десятичные дроби

В данной публикации мы рассмотрим, что из себя представляют бесконечные периодические десятичные дроби, какие бывают виды, и как их можно перевести в обыкновенную дробь. Также разберем примеры для закрепления материала.

Периодические десятичные дроби

Определение

Если в дробной части бесконечной десятичной дроби есть один или несколько цифр, которые повторяются в одной и той же последовательности, такая дробь является периодической.

Примеры периодических десятичных дробей:

Запись

Повторяющаяся цифра/цифры – это период дроби, который пишется в скобке для сокращения длины записи. Например, дроби выше сокращенно следует писать так:

Произношение

• 0,17 (3) – ноль целых, семнадцать сотых и три в периоде;
• 2,45 (29) – две целых, сорок пять сотых и двадцать девять в периоде;
• 4,1038 (476) – четыре целых, тысяча тридцать восемь десятитысячных и четыреста семьдесят шесть в периоде.

Чистые периодические дроби – это такие бесконечные десятичные дроби, период которых начинается сразу после запятой.

Смешанные периодические дроби – бесконечные десятичные дроби, у которых между запятой и периодом присутствует одна и более цифр (их количество ограничено).

Перевод периодической десятичной дроби в обыкновенную

Для того, чтобы перевести периодическую дробь в обыкновенную (простую), выполняем следующие шаги:

1. Считаем количество цифр, содержащихся в периоде дроби. Даем ей буквенное обозначение, например, n .

2. Считаем количество цифр в дробной части между запятой и периодом. Пусть это будет буква m .

3. Составляем из дробной части, в т.ч. из периода, обычное натуральное число. Дадим ему названием a . При этом если первая цифра после запятой – это ноль, его не учитываем.

4. Составляем еще одно число из цифр после запятой, но до периода. Пусть это будет b . Ноль в начале, если он есть, также убираем.

5. Целую часть десятичной дроби примем за x .

6. Итак, обыкновенная дробь y , которую требуется найти, вычисляется по формуле:

Пример 1

Давайте переведем число 0,8(3) в обыкновенную дробь.

Действовать будет пошагово согласно инструкции выше:
1. n = 1
2. m = 1
3. a = 83
4. b = 8
5. x = 0
6. Остается только применить формулу:

Пример 2

Представим периодическую дробь 2,64(378) в виде обыкновенной.

1. n = 3
2. m = 2
3. a = 64378
4. b = 64
5. x = 2
6. Подставляем эти значения в формулу нахождения простой дроби и получаем:

Источник