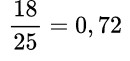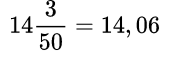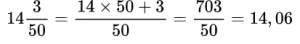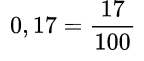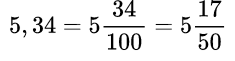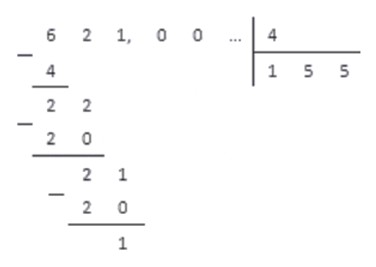Перевод десятичной дроби в обыкновенную и наоборот

Как перевести десятичную дробь в обыкновенную

Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.

Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:

Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?

Основной алгоритм

На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.

Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:

Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:

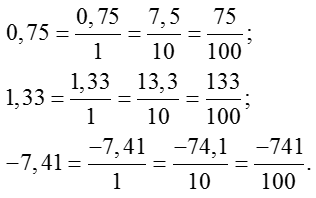Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры: Алгоритм перехода к обычным дробям

Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25. Поэтому получаем $0,75=\frac<75><100>=\frac<3\cdot 25><4\cdot 25>=\frac<3><4>$ — вот и весь ответ.:)

Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:

Примеры перехода от десятичной записи дробей к обычной

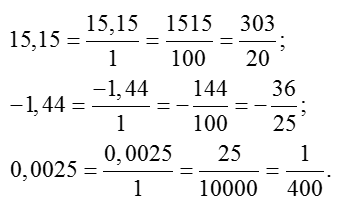
Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?

Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.

Более быстрый способ

В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:

Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:

Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: $<<10>^>=<<10>^<2>>=100$, поэтому в знаменателе стоит именно сто. Ну а затем остаётся лишь сократить числитель и знаменатель.:)

Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на $<<10>^>=<<10>^<3>>=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.

Наконец, последний пример:

Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.

Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Преобразования «на слух»

Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.

А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.

Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:

Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому

А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому

В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому

\[\begin& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end\]

Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.

На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».

Источник

СПАДИЛО.РУ

теория по математике 📈 числа и вычисления

При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует.

Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель. Как перевести обыкновенную дробь в конечную десятичную дробь?

Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик).

Пример №1. ½ = 0,5 так как 1:2=0,5 Пример №2. ¾ = 0,75 так как 3:4=0,75 Пример №3. Так как 18:25=0,72, то

Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.

Пример №4.

здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.

Пример №5.

в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель — это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06.

Как перевести десятичную дробь (конечную) в обыкновенную?

Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь.

Пример №6.

целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля.

Пример №7.

целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь

Источник

Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры

Содержание:

Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.

Перевод обыкновенных дробей в десятичные

Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.

Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.

Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби

Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.

Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.

Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?

Правило перевода обыкновенных правильных дробей в десятичные

1. Записываем 0 и ставим после него запятую.
2. Записываем число из числителя, которое получилось после дописывания нулей.

Теперь перейдем к примерам.

Пример 1. Перевод обыкновенных дробей в десятичные

Переведем обыкновенную дробь 39 100 в десятичную.

Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно — количество цифр в числителе совпадает с количеством нулей в знаменателе.

Следуя правилу, записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 39 .

Разберем решение еще одного примера по этой теме.

Пример 2. Перевод обыкновенных дробей в десятичные

Запишем дробь 105 10000000 в виде десятичной дроби.

Количество нулей в знаменателе равно 7 , а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:

Теперь записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 0000105 .

Рассмотренные во всех примерах дроби — обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.

Правило перевода обыкновенных неправильных дробей в десятичные

1. Записываем число, которое находится в числителе.
2. Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.

Ниже приведем пример на использование этого правила.

Пример 3. Перевод обыкновенных дробей в десятичные

Переведем дробь 56888038009 100000 из обыкновенной неправильной в десятичную.

Сначала запишем число из числителя:

Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе — пять). Получим:

Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.

Правило перевода смешанных чисел в десятичные дроби

1. Выполняем подготовку дробной части числа, если это необходимо.
2. Записываем целую часть исходного числа и ставим после него запятую.
3. Записываем число из числителя дробной части вместе с дописанными нулями.

Обратимся к примеру.

Пример 4. Перевод смешанных чисел в десятичные дроби

Переведем смешанное число 23 17 10000 в десятичную дробь.

В дробной части имеем выражение 17 10000 . Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 0017 10000 .

Теперь записываем целую часть числа и ставим после него запятую: 23 , . .

После запятой записываем число из числителя вместе с нулями. Получаем результат:

23 17 10000 = 23 , 0017

Перевод обыкновенных дробей в конечные и бесконечные периодические дроби

Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.

Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.

Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.

Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.

Числитель при делении представляется в виде десятичной дроби — справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.

Пример 5. Перевод обыкновенных дробей в десятичные

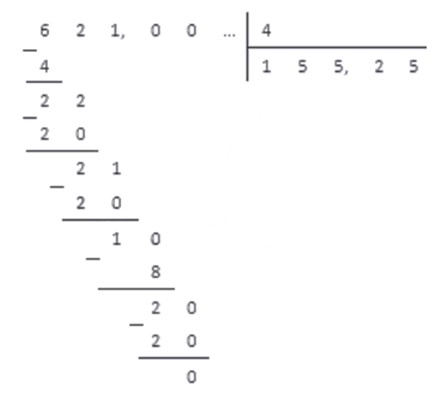
Переведем обыкновенную дробь 621 4 в десятичный вид.

Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621 = 621 , 00

Теперь разделим столбиком 621 , 00 на 4 . Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.

Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.

В итоге мы получаем десятичную дробь 155 , 25 , которая и является результатом обращения обыкновенной дроби 621 4

Рассмотрим решение еще одного примера, чтобы закрепить материал.

Пример 6. Перевод обыкновенных дробей в десятичные

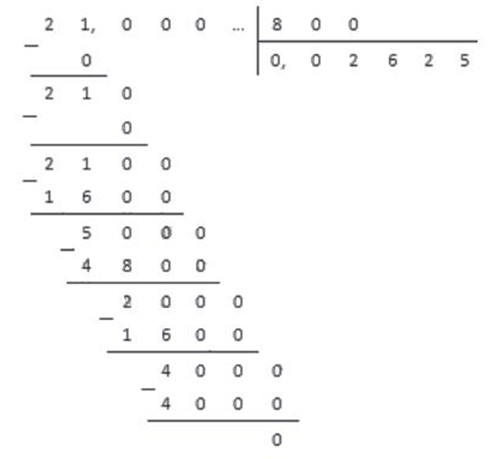
Обратим обыкновенную дробь 21 800 .

Для этого в столбик разделим дробь 21 , 000 на 800 . Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.

В результате мы получили: 21 800 = 0 , 02625 .

Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.

Пример 7. Перевод обыкновенных дробей в десятичные

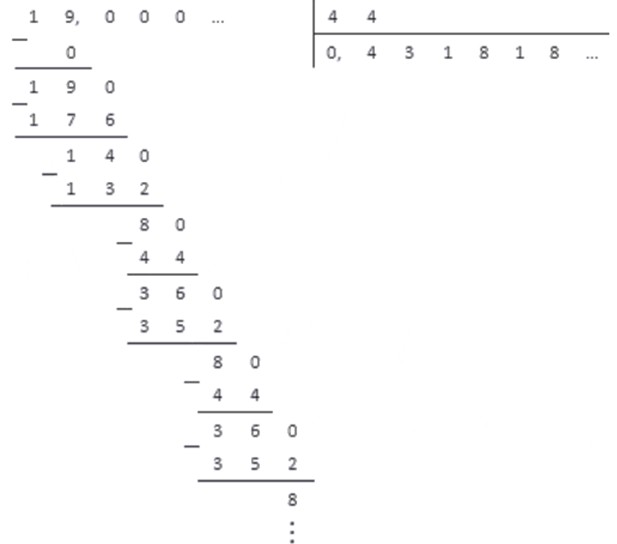
Обратим обыкновенную дробь 19 44 в десятичную. Для этого выполним деление столбиком.

Мы видим, что при делении повторяются остатки 8 и 36 . При этом в частном повторяются цифры 1 и 8 . Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.

Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.

Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие — в бесконечные периодические?

Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000. то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.

1. Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
2. Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.

Пример 8. Перевод обыкновенных дробей в десятичные

Какая из данных дробей 47 20 , 7 12 , 21 56 , 31 17 переводится в конечную десятичную дробь, а какая — только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.

Дробь 47 20 , как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100 .

47 20 = 235 100 . Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.

Разложение знаменателя дроби 7 12 на множители дает 12 = 2 · 2 · 3 . Так как простой множитель 3 отличен от 2 и от 5 , данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.

Дробь 21 56 , во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 3 8 , разложение знаменателя которой на множители дает 8 = 2 · 2 · 2 . Следовательно, это конечная десятичная дробь.

В случае с дробью 31 17 разложение знаменателя на множители представляет собой само простое число 17 . Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.

Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь

Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?

При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.

Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:

1. Мы получаем в остатке 0, и на этом деление заканчивается.
2. Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.

Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.

Перевод десятичных дробей в обыкновенные дроби

Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?

Правило перевода десятичных дробей в обыкновенные дроби

1. В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
2. В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
3. При необходимости сокращаем полученную обыкновенную дробь.

Рассмотрим применение данного правила на примерах.

Пример 8. Перевод десятичных дробей в обыкновенные

Представим число 3 , 025 в виде обыкновенной дроби.

1. В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
2. В знаменателе пишем единицу, а после нее три нуля — именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
3. Полученную дробь 3025 1000 можно сократить на 25 , в результате чего мы получим: 3025 1000 = 121 40 .

Переведем дробь 0 , 0017 из десятичных в обыкновенные.

1. В числителе запишем дробь 0 , 0017 , отбросив запятую и нули слева. Получится 17 .
2. В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000 . Данная дробь несократима.

Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?

Сформулируем еще одно правило.

Правило перевода десятичных дробей в смешанные числа.

1. Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
2. В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
3. В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.

Обратимся к примеру

Пример 10. Перевод десятичной дроби в смешанное число

Представим дробь 155 , 06005 в виде смешанного числа.

1. Записываем число 155 , как целую часть.
2. В числителе записываем цифры после запятой, отбросив нуль.
3. В знаменателе записываем единицу и пять нулей

Поучаем смешанное число: 155 6005 100000

Дробную часть можно сократить на 5 . Сокращаем, и получаем финальный результат:

155 , 06005 = 155 1201 20000

Перевод бесконечных периодических десятичных дробей в обыкновенные дроби

Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.

Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример 11. Перевод периодической десятичной дроби в обыкновенную

Обратим периодическую дробь 3 , 75 ( 0 ) .

Отбросив нули справа, получим конечную десятичную дробь 3 , 75 .

Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:

3 , 75 ( 0 ) = 3 , 75 = 375 100 = 15 4 .

Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:

0 , ( 74 ) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .

Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b , а знаменатель q таков, что 0 q 1 , то сумма равна b 1 — q .

Рассмотрим несколько примеров с применением данной формулы.

Пример 12. Перевод периодической десятичной дроби в обыкновенную

Пусть у нас есть периодическая дробь 0 , ( 8 ) и нам нужно перевести ее в обыкновенную.

0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . .

Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0 , 8 и знаменателем 0 , 1 .

0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 — 0 , 1 = 0 , 8 0 , 9 = 8 9

Это и есть искомая обыкновенная дробь.

Для закрепления материала рассмотрим еще один пример.

Пример 13. Перевод периодической десятичной дроби в обыкновенную

Обратим дробь 0 , 43 ( 18 ) .

Сначала записываем дробь в виде бесконечной суммы:

0 , 43 ( 18 ) = 0 , 43 + ( 0 , 0018 + 0 , 000018 + 0 , 00000018 . . )

Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:

0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 — 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .

Полученное прибавляем к конечной дроби 0 , 43 = 43 100 и получаем результат:

0 , 43 ( 18 ) = 43 100 + 18 9900

После сложения данных дробей и сокращения получим окончательный ответ:

В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.

Источник