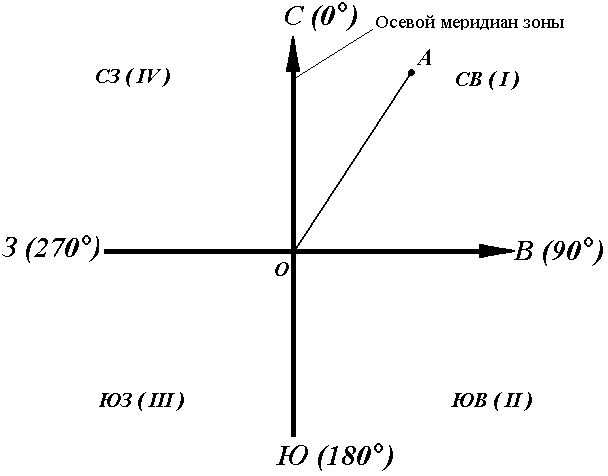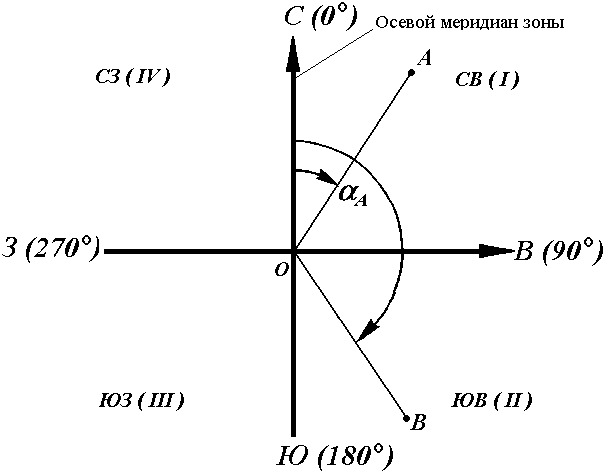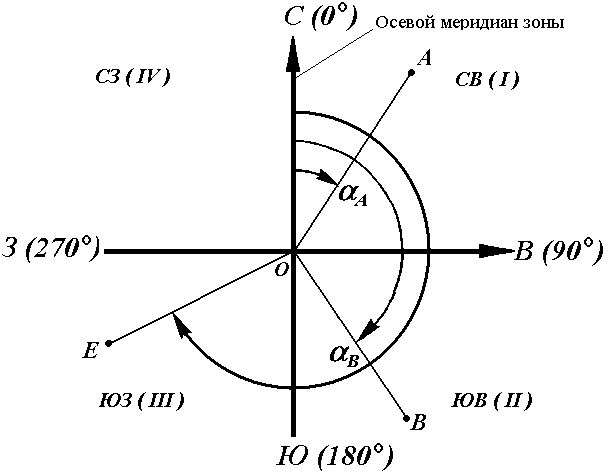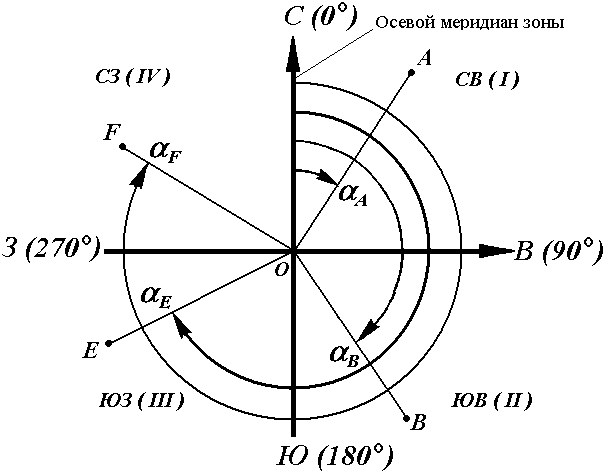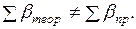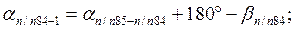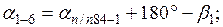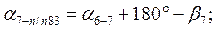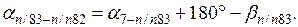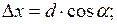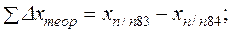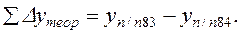Перевод дирекционных углов в румбы
| Номер четверти | Название четверти | Формула перевода |
| I | СВ | rI=α |
| II | ЮВ | rII=180º-α |
| III | ЮЗ | rIII=α-180º |
| IV | СЗ | rIV=360º-α |
Координаты точки п/п83 вычисляют по формулам
; (1.5)
, (1.6)
; (1.7)
. (1.8)
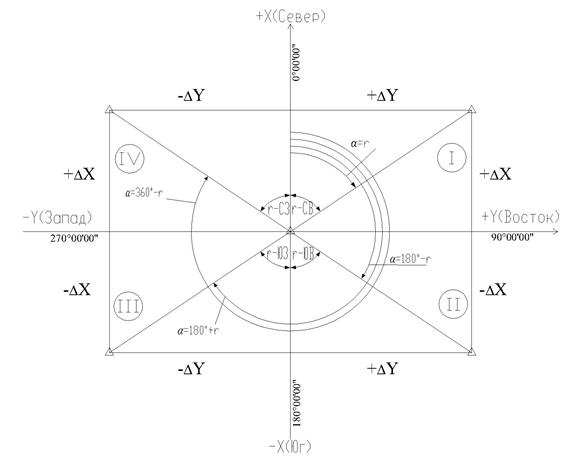
Для удобства вычислений дирекционный угол можно предварительно перевести в румб, пользуясь рис. 1.2 и табл. 1.1.
Рис. 1.2. Зависимость между дирекционными углами и румбами
При использовании румбов знак приращений координат ставят в соответствии с названием румба (табл. 1.2).
Знаки приращений прямоугольных координат
| Приращения | Названия румбов | |||
| СВ | ЮВ | ЮЗ | СЗ | |
| ∆x | + | — | — | + |
| ∆y | + | + | — | — |
;
;
;
;
;
.
Обработка результатов топографической съемки
Участка местности
Исходные данные. Для съемки участка на местности проложен высотно-теодолитный ход между двумя пунктами полигонометрии п/п84 и п/п83. Схема сети и результаты полевых измерений выдаются преподавателем и являются общими для всех вариантов. Для примера, рассмотренного в учебно-методическом пособии, схема сети приведена на рис. 1.3. В ходе измерены длины линий и горизонтальные углы, лежащие справа по ходу. Результаты измерения горизонтальных углов и длин линий для сети, изображенной на рис. 1.3, приведены в табл. 1.3.
Результаты измерений горизонтальных углов и длин сторон хода
| Номера вершин хода | Измеренные углы (правые) | Горизонтальные проложения d, м |
| º | ´ | ´´ |
| п/п84 | 68,74 | |
| 190,36 | ||
| 104,18 | ||
| 110,05 | ||
| п/п83 |
Координаты исходных пунктов п/п84 и п/п83 берутся из подраздела 1.1 (задача 2). Высоты точек п/п84 и п/п83 вычисляются:
; (1.9)
. (1.10)
Иванов Иван ПГСз – 06-50 Н п/п 84 =150,150 м.
Селиванов Сергей АДз – 05-76 Н п/п 84=176,176 м.
Рис. 1.3. Схема планового и высотного обоснований
Задание выполняется в следующей последовательности:
1. Обработка ведомости вычисления координат вершин теодолитного хода.
2. Обработка результатов вычисления высот точек съемочного обоснования.
3. Обработка результатов тахеометрической съемки (обработка журнала тахеометрической съемки).
4. Составление топографического плана.
Обработка ведомости вычисления координат вершин
Теодолитного хода
Обработка ведется в специальной ведомости (табл. 1.4) в следующей последовательности:
1. В графе 4 записывают исходный дирекционный угол начальной стороны αп/п85 – п/п84и исходный дирекционный угол конечной стороны α п/п83 – п/п82.
Исходные дирекционные углы выделены жирным шрифтом. Для рассматриваемого примера 
; 
. Студент исходные данные своего варианта берет из задачи 1 подраздела 1.1.
2. Вычисляется сумма измеренных углов в ходе (значения измеренных углов записаны в графе 2) – 
. Для рассматриваемого примера 
.
Если через 
и 
обозначим дирекционные углы в начале и конце теодолитного хода, которые заданы как неизменные и безошибочные, то в этом случае должно выполняться равенство
, (1.11)
где n – число вершин, на которых измерялись углы.
Если это равенство переписать для 
, то полученное выражение можно использовать для вычисления теоретической суммы углов в ходе. Отсюда
= 
. (1.12)
Дирекционные углы и осевые румбы
Лекция 6
Ориентирование линии. Прямая и обратная геодезические задачи.
При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.
Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.
В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.
Дирекционные углы и осевые румбы
Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).
Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.
Рис. 16. Дирекционные углы
Для линии ОА её дирекционным углом в точке О является горизонтальный угол αОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – αОВ , αОE , αОF.
Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.
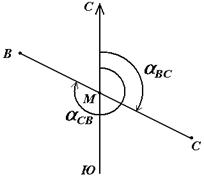
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке.
Рис. 17. Прямое и обратное направление линии
Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.
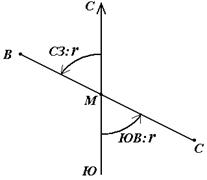
Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).
Осевым румбомназывается острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.
Рис. 18. Румбы и дирекционные углы
Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).
Зависимость между дирекционными углами и румбамиопределяется для четвертей по следующим формулам:
I четверть (СВ) r = α
II четверть (ЮВ) r = 180° – α
III четверть (ЮЗ) r = α – 180°
IV четверть (СЗ) r = 360° – α
Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.
Перевод дирекционных углов в румбы
| Номер четверти | Название четверти | Формула перевода |
| I | СВ | rI=α |
| II | ЮВ | rII=180º-α |
| III | ЮЗ | rIII=α-180º |
| IV | СЗ | rIV=360º-α |
Координаты точки п/п83 вычисляют по формулам
; (1.5)
, (1.6)
; (1.7)
. (1.8)
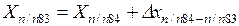
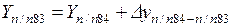
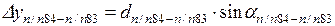
Для удобства вычислений дирекционный угол можно предварительно перевести в румб, пользуясь рис. 1.2 и табл. 1.1.
Рис. 1.2. Зависимость между дирекционными углами и румбами
При использовании румбов знак приращений координат ставят в соответствии с названием румба (табл. 1.2).
Знаки приращений прямоугольных координат
| Приращения | Названия румбов | |||
| СВ | ЮВ | ЮЗ | СЗ | |
| ∆x | + | — | — | + |
| ∆y | + | + | — | — |
;
;
;
;
;
.
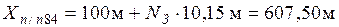
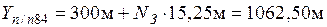
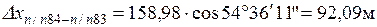
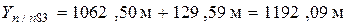
Обработка результатов топографической съемки
Участка местности
Исходные данные. Для съемки участка на местности проложен высотно-теодолитный ход между двумя пунктами полигонометрии п/п84 и п/п83. Схема сети и результаты полевых измерений выдаются преподавателем и являются общими для всех вариантов. Для примера, рассмотренного в учебно-методическом пособии, схема сети приведена на рис. 1.3. В ходе измерены длины линий и горизонтальные углы, лежащие справа по ходу. Результаты измерения горизонтальных углов и длин линий для сети, изображенной на рис. 1.3, приведены в табл. 1.3.
Результаты измерений горизонтальных углов и длин сторон хода
| Номера вершин хода | Измеренные углы (правые) | Горизонтальные проложения d, м |
| º | ´ | ´´ |
| п/п84 | 68,74 | |
| 190,36 | ||
| 104,18 | ||
| 110,05 | ||
| п/п83 |
Координаты исходных пунктов п/п84 и п/п83 берутся из подраздела 1.1 (задача 2). Высоты точек п/п84 и п/п83 вычисляются:
; (1.9)
. (1.10)
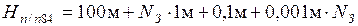
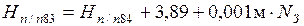
Иванов Иван ПГСз – 06-50 Н п/п 84 =150,150 м.
Селиванов Сергей АДз – 05-76 Н п/п 84=176,176 м.
Рис. 1.3. Схема планового и высотного обоснований
Задание выполняется в следующей последовательности:
1. Обработка ведомости вычисления координат вершин теодолитного хода.
2. Обработка результатов вычисления высот точек съемочного обоснования.
3. Обработка результатов тахеометрической съемки (обработка журнала тахеометрической съемки).
4. Составление топографического плана.
Обработка ведомости вычисления координат вершин
Теодолитного хода
Обработка ведется в специальной ведомости (табл. 1.4) в следующей последовательности:
1. В графе 4 записывают исходный дирекционный угол начальной стороны αп/п85 – п/п84и исходный дирекционный угол конечной стороны α п/п83 – п/п82.
Исходные дирекционные углы выделены жирным шрифтом. Для рассматриваемого примера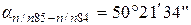 
; 
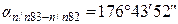
. Студент исходные данные своего варианта берет из задачи 1 подраздела 1.1.
2. Вычисляется сумма измеренных углов в ходе (значения измеренных углов записаны в графе 2) –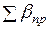 
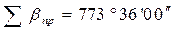
. Для рассматриваемого примера 
.
Если через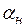 
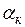
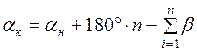
и 
обозначим дирекционные углы в начале и конце теодолитного хода, которые заданы как неизменные и безошибочные, то в этом случае должно выполняться равенство
, (1.11)
где n – число вершин, на которых измерялись углы.
Если это равенство переписать для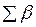 
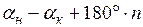
, то полученное выражение можно использовать для вычисления теоретической суммы углов в ходе. Отсюда
= 
. (1.12)
Ведомость вычисления прямоугольных координат
Вершин теодолитного хода
| Номера точек | Измерен- ные углы bi | Исправлен- ные углы bиспр | Дирекцион- ные углы ai | Румбы ri |
| ° ‘ » | ° ‘ » | ° ‘ » | назв. | ° ‘ » |
| п/п85 | — | — | ||
| 50 21 34 | СВ | 50 21 34 | ||
| п/п84 | 202 48 00 | 202 48 20 | ||
| 27 33 14 | СВ | 27 33 14 | ||
| 199 12 30 | 199 12 51 | |||
| 8 20 23 | СВ | 8 20 23 | ||
| 70 10 00 | 70 10 20 | |||
| 118 10 03 | ЮВ | 61 49 57 | ||
| 106 46 30 | 106 46 51 | |||
| 191 23 12 | ЮЗ | 11 23 12 | ||
| п/п83 | 194 39 00 | 194 39 20 | ||
| 176 43 52 | ЮВ | 03 16 08 | ||
| п/п82 | ||||
 |
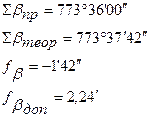| Горизон-тальное проло- жение | Приращения координат, м | Координаты, м | ||||||||
| вычисленные | исправленные | |||||||||
| d, м | + — | Δx | + — | Δy | + — | Δx | + — | Δy | x | y |
| 607,50 | 1062,50 | |||||||||
| 68,74 | + | -0,02 60,94 | + | +0,01 31,80 | + | 60,92 | + | 31,81 | ||
| 668,42 | 1094,31 | |||||||||
| 190,36 | + | -0,06 188,35 | + | +0,03 27,61 | + | 188,29 | + | 27,64 | ||
| 856,71 | 1121,95 | |||||||||
| 104,18 | — | -0,03 49,18 | + | +0,01 91,84 | — | 49,21 | + | 91,85 | ||
| 807,50 | 1213,80 | |||||||||
| 110,05 | — | -0,03 107,88 | — | +0,02 21,73 | — | 107,91 | — | 21,71 | ||
| 699,59 | 1192,09 | |||||||||
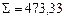 м |  |  |  |  | ||||||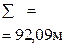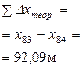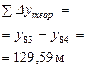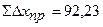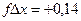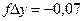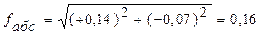
  м   м 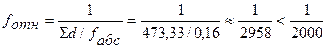 м  м |
Для рассматриваемого примера 
.
В нашем примере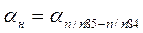 
; 
.
Вследствие ошибок измерений углов практическая сумма измеренных горизонтальных углов не равна теоретической сумме горизонтальных углов, разность между ними называют угловой невязкой.
3. Вычисляется угловая невязка хода. Разница между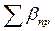 
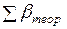
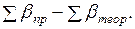
и 
и составляет угловую невязку в разомкнутом теодолитном ходе.
= 
(1.13)
Полученную невязку сравнивают с допустимой, которая вычисляется по формуле
(1.14)
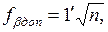
где n – число измеренных углов.
В нашем примере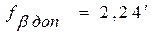 
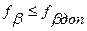
. Если выполняется неравенство 
, то делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:
. (1.15)
Поправки вычисляются до целых секунд. Должно выполняться равенство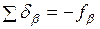 
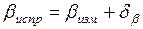
. К измеренным углам прибавляют поправку со своим знаком, результат записывают в графу 3. 
. (1.16)
Контролем правильности исправления углов служит равенство
. (1.17)
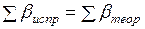
После уравнивания углов вычисляют дирекционные углы всех сторон хода по формуле
(1.18)
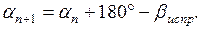
Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус правый (исправленный) угол хода, образованный этими сторонами.
Для нашего хода вычисления ведут в следующей последовательности:
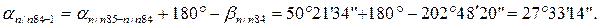
Вычисленный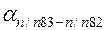 
должен быть точно равен исходному 
. Результаты вычислений записывают в графу «Дирекционные углы».
Если при вычислении дирекционный угол получается отрицательным, то кроме 180º к дирекционному углу предыдущей стороны необходимо прибавить 360º. Если дирекционный угол получается больше 360º, то из него вычитают 360º.
4. Производят уравнивание линейных измерений. Обработка линейных измерений начинается с вычисления приращений координат для всех сторон теодолитного хода по формулам
, (1.19)
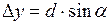
где d – горизонтальное проложение стороны хода;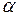 
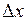
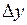
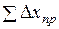
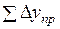
– дирекционный угол этой же стороны.
Вычисленные приращения координат ( 
и 
) записывают в графы 9 и 11 табл. 1.4, находят их суммы 
, 
и приступают к их уравниванию.
Зная координаты начальной точки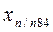 
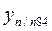
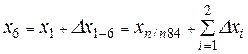
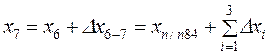
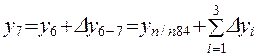
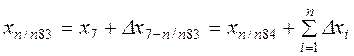
и 
и приращения, можно вычислить координаты всех точек теодолитного хода:
; 
;
; 
;
; 
;
; 
,
где п – число измеренных сторон хода.
Из последней строки системы определим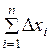 
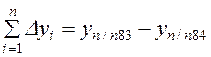
и 
:
; 
. (1.20)
Или в общем виде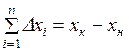 
; 
.
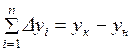
Эти формулы справедливы тогда, когда приращения координат не имеют погрешностей. Поэтому суммы данных приращений называют теоретическими и обозначают через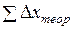 
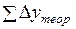
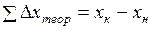
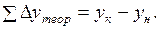
и 
, т.е.
; 
(1.21)
Для нашего примера
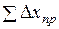
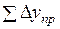
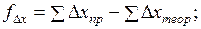
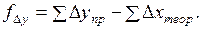
Так как измерения длин сторон имеют погрешности, то суммы вычисленных приращений ( , ) координат отличаются от теоретического значения. Разности этих величин называютневязками приращений.
(1.22)
Невязки 
и 
показывают отклонение вычисленных координат конечной точки от её теоретического положения соответственно по осям 
и 
.
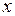
Для оценки точности используют линейную невязку, т.е. расстояние меж 
ду этими точками (рис. 1.4). Линейную величину 
невязки определим как гипотенузу прямоугольного треугольника с катетами и .
(1.23)
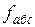
Наилучшим образом точность измерений в ходе характеризует относительная невязка, т.е. величина линейной невязки, отнесённая ко всему периметру полигона.
, (1.24)
, (1.25)
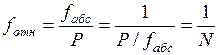
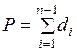
здесь п – число измерений сторон хода; Р – длина хода.
Относительную невязку принято записывать в виде дроби с единицей в числителе, что облегчает сравнение двух или нескольких значений. Качество измерений в теодолитном ходе считают удовлетворительным, если 
.
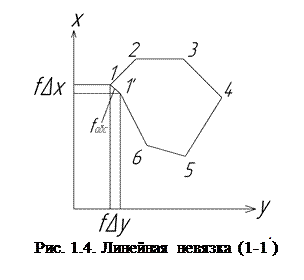
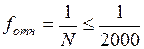
Если полученная относи-тельная невязка не превышает допустимого значения, то невязки и 
распределяют между приращениями координат.
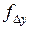
Примеры в задании подобраны так, чтобы относительная невязка получилась допустимой. Если относительная невязка оказалась недопустимой, то в вычислениях допущены ошибки.
Дирекционные углы сторон хода вычислены по исправленным значениям горизонтальных углов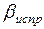 
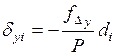
. Следовательно, появление невязок вызвано погрешностями измерения длин сторон хода. Кроме того, погрешность измерения стороны хода пропорциональна её длине (т.е. чем больше длина стороны, тем большая вероятность появления погрешности в её измерении), поэтому невязки в приращениях координат распределяют пропорционально длинам сторон, для этого в каждое приращение вычисляют поправку по формулам
; 
. (1.26)
Контролем правильности распределения поправок являются равенства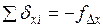 
; 
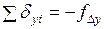
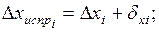
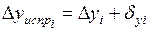
. Далее вычисляют исправленные значения приращений координат
. (1.27)
Контролем вычислений служит выполнение равенства
; 
. (1.28)
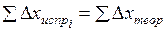
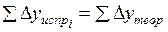
Для разомкнутого теодолитного хода
, (1.29)
(1.30)
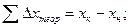
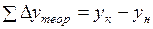
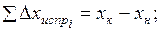
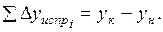
Вычисление координат точек теодолитного хода производят по формулам
 ;  ; ………………………  ; |  ;  ; ……………………….  . |
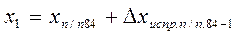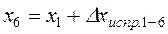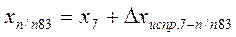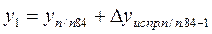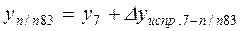Получение xп/п83и yп/п83, равных исходным значениям, служит контролем правильности вычисления координат точек теодолитного хода.