Перевод дробных чисел из одной системы счисления в другую
Перевод дробных чисел из одной системы счисления в другую
После того, как я сделал несколько калькуляторов для перевода между разными системами счисления — вот список от первой до последней версии, от самого простого к сложному: Перевод числа в другие системы счисления, Перевод из десятичной системы счисления, Перевод из одной системы счисления в другую — в комментариях стали периодически спрашивать — а что же, мол, дробные числа, как же их переводить? И когда спросили больше трех раз, я таки решил изучить этот вопрос.
Результатом стал калькулятор, который вы видите ниже, он умеет переводить и дробные числа в том числе. Как водится, для любознательных под калькулятором немного теории.
Перевод дробных чисел из одной системы счисления в другую
Теперь теория. Я, честно говоря, думал, что вопрос довольно сложный, но при ближайшем рассмотрении все оказалось проще простого. Надо было только держать в голове тот факт, что речь идет о позиционных системах счисления.
В чем тут суть? Рассмотрим на примере десятичного числа 6.125. Это дробное число в десятичной системе счисления представляется так:
Все просто, не так ли? Та же самая простота сохраняется и при записи дробного числа в любой другой системе счисления. Возьмем, например, горячо любимую каждым программистом двоичную систему и число, например, 110.001. Эта запись есть не что иное как
Да-да, число для примера было выбрано не просто так. То есть, 110.001 в двоичной системе есть 6.125 в десятичной. Принцип, я думаю, ясен.
Есть только одно но — все-таки из-за того, что здесь участвую дроби с разными знаменателями, не всегда одно и тоже число можно одинаково точно выразить в разных системах счисления. Что я имею в виду?
Возьмем, например, число . Отлично смотрится в десятичной системе счисления. Но вот если попробовать получить запись этого числа в двоичной системе счисления — будут проблемы. Попробуем, пока не устанем
Продолжать можно еще довольно долго, но уже сейчас видно, что 0.8 в десятичной системе это 0.11001100. (дальше очень много цифр) в двоичной. Если честно, то это периодическое число с перидом 1100, так что мы никогда не сможем выразить его точно в двоичной системе счисления. 110011001100. будет продолжаться до бесконечности.
Поэтому перевод дробного числа из одной системы счисления в другую чаще всего дает погрешность. Погрешность эта зависит от того, сколько разрядов мы используем для записи дробной части переведенного числа. Возьмем пример с числом 0.8 и используем для записи его двоичного представления шесть разрядов после запятой — 0.110011. Полученное число вовсе не 0.8, а 0.796875, разница при этом составляет 0.003125. Это и есть наша погрешность перевода десятичного числа 0.8 в двоичный вид при использовании шести разрядов после запятой.
Вес крайнего правого разряда (самого младшего разряда) называется разрешением (resolution) или точностью (precision), и определяет наименьшее неравное нулю число, которое может быть представлено данным числом разрядов. Для нашего примера это . При этом максимально возможная погрешность представления числа, как нетрудно сообразить, не превышает половины этого веса, или 0.0078125. Так что для 0.8 мы имеем еще и не самую плохую погрешность.
Преобразование дробных двоичных чисел в десятичные



Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:
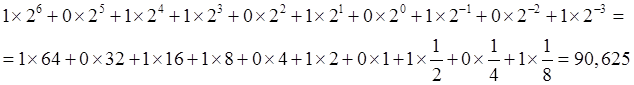
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
- Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
- Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
- В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
- Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232
.232 • 2 = 0.464
.464 • 2 = 0.928
.928 • 2 = 1.856
.856 • 2 = 1.712
.712 • 2 = 1.424
.424 • 2 = 0.848
.848 • 2 = 1.696
.696 • 2 = 1.392
.392 • 2 = 0.784
и т. д.
Получим: 206,11610=11001110,00011101102
· Преобразование восьмеричных чисел в десятичные.
Алгоритм перевода чисел из восьмеричной в десятичную систему счисления аналогичен уже рассматривавшему мною в разделе: Преобразование двоичных чисел в десятичные.
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет[1] двоичных цифр.
Пример: 25418 = 010 101 100 001 = 0101011000012
Существует таблица перевода восьмеричных чисел в двоичные
| 08 | = | 0002 |
| 18 | = | 0012 |
| 28 | = | 0102 |
| 38 | = | 0112 |
| 48 | = | 1002 |
| 58 | = | 1012 |
| 68 | = | 1102 |
| 78 | = | 1112 |
· Преобразование шестнадцатеричных чисел в десятичные.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·16 0 +10·16 1 +5·16²= 3·1+10·16+5·256= 3+160+1280= 144310
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
0101101000112 = 0101 1010 0011 = 5A316
Перевод дробных чисел из десятичной системы счисления в двоичную
Перевод чисел из различных систем счисления в двоичную сводится к их представлению в виде различных комбинаций двух цифровых символов этой системы – 0 и 1. Для перевода из десятичной системы в двоичную чаще всего используется метод последовательного деления на 2, где 2 – это разряд двоичного кода аналогично 10 в десятичном счислении.
Однако этот метод подходит при переводе целых чисел, для дробей же используют, напротив, умножение. А именно умножают дробную часть на 2 последовательно до тех пор, пока не появится целая часть. При этом удачное умножение, дающее в результате число, большее 1, приносит итоговому двоичному числу цифру 1. А неудачное, после которого число все еще меньше 1, дает цифру 0. При этом цифры дроби в двоичном виде записываются после запятой также, как в исходной десятичной.
3Рассмотрим этот немудреный способ на конкретном примере. Для начала возьмите простую десятичную дробь 0,2. Умножайте последовательно на 2:0,2*2 = 0,4 => 0,0_2;0,4*2 = 0,8 => 0,00_2;0,8*2 = 1,6 => 0,001_2;
Отбросьте целую часть и продолжайте те же действия:0,6*2 = 1,2 => 0,0011_2;Снова отбросьте целую часть и вы вернетесь к числу 0,2. Двоичная дробь оказалась цикличной, т.е. повторяющейся, сокращенно запишите:0,2_10 = 0,(0011)_2, где скобки указываются на повторяемость одной и той же группы цифр.
Таким образом,для перевода в двоичную систему дроби с целой частью сначала переводится именно она, а потом уже число после запятой. Например, переведите число 9,25.Для перевода целой части воспользуйтесь методом последовательного деления: 9/2 = 4 и 1 в остатке;4/2 = 2 и 0 в остатке;2/2 = 1 и 0 в остатке;½ = 0 и 1 в остатке. Запишите полученные остатки справа налево: 9_10 = 1001_2.
6Теперь переведите дробную часть:0,25*2 = 0,5 => 0;0,5*2 = 1 => 1.На этот раз вам повезло, дробь оказалась не цикличной. Запишите итог:9,25_10 = 1001,01_2.
Перевод десятичных дробей в двоичную систему счисления заключается в поиске целых частей при умножении на 2. Например, переведём десятичную дробь 0,625 в двоичную систему счисления. Чтобы найти первую после запятой цифру двоичной дроби, нужно умножить заданное число на 2 и выделить целую часть произведения.
0,625 · 2 = 1,250 (целая часть равна 1);
0,250 · 2 = 0,500 (целая часть равна 0);
0,500 · 2 = 1,000 (целая часть равна 1).
Дробная часть последнего произведения равна 0. Перевод закончен. Записываем в одну строку полученное значение целой части, начиная с первой цифры: 0,62510 = 0,1012. Каждый раз в умножении участвует только дробная часть десятичного числа.
Правило перевода: Чтобы перевести положительную десятичную дробь в двоичную, нужно дробь умножить на 2. Целую часть произведения взять в качестве первой цифры после запятой в двоичной дроби, а дробную часть вновь умножить на 2. В качестве следующей цифры взять целую часть этого произведения, а дробную часть произведения снова умножить на 2 и т.д.
При переводе десятичной дроби в двоичную может получиться периодическая дробь.
Пример. Переведем десятичную дробь 0,3 в двоичную систему счисления.
0,3 · 2 = 0,6 (целая часть равна 0);
0,6 · 2 = 1,2 (целая часть равна 1);
0,2 · 2 = 0,4 (целая часть равна 0);
0,4 · 2 = 0,8 (целая часть равна 0);
0,8 · 2 = 1,6 (целая часть равна 1);
0,6 · 2 = 1,2 (целая часть равна 1);
Дробная часть 0,6 уже была на втором шаге вычислений, поэтому вычисления начнут повторяться. Следовательно, в двоичной системе счисления число 0,3 представляется периодической дробью.
Ответ: 0,310 = 0,0(1001)2.
Перевод конечных дробей в позиционных системах счисления
Для перевода правильных дробей из десятичной системы счисления в систему счисления с основанием S нужно умножать исходную дробь последовательно на основание системы счисления S. Полученные в результате умножения целые части произведения являются соответствующими разрядами дробного числа в системе счисления с основанием S.
Перевод правильной конечной р-ичной дроби в десятичную систему счисленияосуществляется аналогично переводу целого числа через развернутую форму представления числа.
Замечание.
При вычислении десятичного значения р-ичной дроби по развернутой форме с использованием калькулятора также целесообразно пользоваться схемой Горнера, что минимизирует количество арифметических действий и исключает возведение в степень.
Алгоритм перевода конечной р-ичной дроби в десятичную СС:
1. Целая часть числа переводится в десятичную систему отдельно от дробной части, согласно правилам перевода.
2. Каждая цифра дробной части р-ичного числа переводится в десятичную систему.
3. Полученные числа нумеруются слева направо, начиная с единицы.
4. Число Р переводится в десятичную систему.
5. Десятичное число, соответствующее каждой р-ичной цифре, умножаются на р — k , где k – номер этого числа, результаты складываются по правилам десятичной системы.
Контрольные вопросы:
1. Что обеспечивает система счисления?
2. Какая система счисления называется позиционной?
3. Какая система счисления называется непозиционной?
4. Какое равенство отожествляется с позиционной системой счисления?
5. Приведите примеры позиционных и непозиционных систем счисления.
6. Какая арифметика называется недесятичной?
7. Как производится сложение, вычитание, умножение, и деление в двоичной системе счисления?
8. Как производится сложение, вычитание, умножение, и деление в восьмеричной системе счисления?
9. Как производится сложение, вычитание, умножение, и деление в шестнадцатеричной системе счисления?




