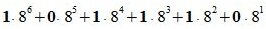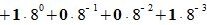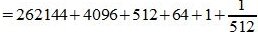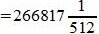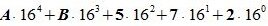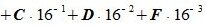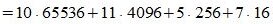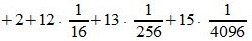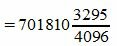Перевод чисел из одной системы счисления в другую онлайн
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
где Цn-целое число в позиции n, Д-k— дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр <0,1,2,3,4,5,6,7,8,9>, в восьмеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7>, в двоичной системе счисления — из множества цифр <0,1>, в шестнадцатеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F>, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1·2 6 + 0 ·2 5 + 1·2 4 + 1·2 3 + 1·2 2 + 0·2 1 + 1·2 0 + 0·2 -1 + 0·2 -2 + 1·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C— на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||
| 158 | 79 | 2 | |
| 1 | 78 | 39 | 2 |
| 1 | 38 | 19 | 2 |
| 1 | 18 | 9 | 2 |
| 1 | 8 | 4 | 2 |
| 1 | 4 | 2 | 2 |
| 0 | 2 | 1 | |
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | |
| x | 2 |
| 0 | 0.428 |
| x | 2 |
| 0 | 0.856 |
| x | 2 |
| 1 | 0.712 |
| x | 2 |
| 1 | 0.424 |
| x | 2 |
| 0 | 0.848 |
| x | 2 |
| 1 | 0.696 |
| x | 2 |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | |
| x | 2 |
| 0 | 0.25 |
| x | 2 |
| 0 | 0.5 |
| x | 2 |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | |
| x | 16 |
| 3 | 0.424 |
| x | 16 |
| 6 | 0.784 |
| x | 16 |
| 12 | 0.544 |
| x | 16 |
| 8 | 0.704 |
| x | 16 |
| 11 | 0.264 |
| x | 16 |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | |
| x | 8 |
| 4 | 0.096 |
| x | 8 |
| 0 | 0.768 |
| x | 8 |
| 6 | 0.144 |
| x | 8 |
| 1 | 0.152 |
| x | 8 |
| 1 | 0.216 |
| x | 8 |
| 1 | 0.728 |
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Позиционные системы счисления. Перевод целых и дробных чисел из десятичной в двоичную систему счисления и обратно.
Позиционные системы счисления. Перевод целых и дробных чисел из десятичной в двоичную систему счисления и обратно.
Позиционная система счисления— система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией.
Перевод целых чисел из 10 в 2 систему счисления и обратно
Необходимо последовательно делить х и получаемые частные на n (основание новой системы) до тех пор, пока не получится частное меньше n.
Запись: последнее частное и остатки от деления, записываемые в обратной последовательности.
Перевод из любой позиционной системы в десятичную выполняется, используя разложение по степеням основания.
Переводы дробных чисел из 10 в 2 систему счисления
Разложение числа по степеням основания
· Вначале переводится целая часть десятичной дроби в двоичную с.с.
· Затем, дробная часть десятичной дроби умножается на основание двоичной с.с.
· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной с.с.
· Алгоритм завершается, если дробная часть полученного произведения равна 0 или, если достигнута требуемая точность вычисления. В противном случае, вычисления продолжаются с предыдущего шага.
Перевод из двоичной в восьмеричную и шестнадцатеричную системы счисления.
Для перевода двоичного числа в восьмеричное:
· Разделить число на триады ( если оно десятичное, то влево от запятой и вправо от запятой)
· Заменить каждую триаду двоичных чисел соответствующей восьмеричной цифрой по таблице
· Недостающие до триады позиции заполнить незначащими нулями
Для переводя двоичного числа в шестнадцатеричное воспользуемся тем же алгоритмом, но число будем делить на тетрады.
Пример: 1111010,01111112=7А,7Е16 и наоборот 7А,7Е16 = 1111010,01111112
Классификация ЭВМ
ЭВМ (Электронно-вычислительная машина)– комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач.
1. По принципу действия:
-вычислительные машины дискретного действия (цифровые)
-аналоговые ( представляет данные в непрерывной форме с помощью физических переменных: скорость, длина, напряжение, ток)
-проблемно-ориентированные (разрабатывают конструктор, например)
-специализированные (только определенный круг задач)
3. По поколению ( по этапам создания)
-физический элемент (ламповые)
-быстродействие ( количество операций умножения над вещественными числами, которые выполняются каждую секунду)
Структурная схема ПК
ПК (Персональный компьютер) – универсальная ЭВМ, предназначенная для индивидуального пользования
МП (микропроцессор)- основное устройство ЭВМ, выполняет команды программы и управляет взаимодействием всех компонентов ЭВМ.
ПЗУ (постоянное запоминающее устройство)- хранит программы, выполняет загрузки операционных систем компьютеров.
ОЗУ (оперативное запоминающее устройство) –хранит программы и данные, которые выполняют в данный момент на ЭВМ.
Системная шина- набор проводов, которые позволяют осуществлять связь между разными частями.
ВК (видеокарта)- дополнительное устройство, которое формирует изображение и передает его на монитор.
КК (контроллер клавиатуры)- содержит буфер(память), в которые помещены отдельные символы, и передает их другим компонентам.
СА (сетевой адаптер) – обеспечивает обмен информацией с локальными и глобальными компьютерными сетями.
ВЗУ (внешнее запоминающее устройство) –жесткий диск, Flash память.
ПУ (периферийное устройство различного назначения) – принтеры, сканеры.
КВЗУ (контроллер внешних запоминающих устройств)-управляет обменом информации с МП или ПЗУ.
КПВВ (контроллер портов ввода/вывода)- управляет обменом информации с ПУ или ПЗУ.
ИП — источник питания.
Системная шина
СШ (системная шина)- служит для обмена командами и данными между компонентами ЭВМ.
Системная шина включает в себя:
· шину данных для параллельной передачи всех разрядов операнда из ОЗУ в МП и обратно; имеет 64 разряда
· шину адреса для параллельной передачи всех разрядов адреса ячейки ОЗУ; имеет 32 разряда
· шину инструкций для передачи команд во все блоки ЭВМ; простые команды кодируются одним байтом, но есть и команды, кодируемые двумя, тремя и более байтами; имеет 32 разряда
· шину питания для подключения блоков ЭВМ к системе энергопитания.
Системная шина обеспечивает три направления передачи информации:
2) между МП и контроллерами устройств;
3) между ОЗУ и внешними устройствами (ВЗУ и ПУ, в режиме прямого доступа к памяти).
Все устройства подключаются к системной шине через контроллеры – устройства, которые обеспечивают взаимодействие внешних устройств и системной шины.
Характеристики системной шины:
· количество обслуживаемых ею устройств
· пропускная способность (максимальная возможная скорость передачи информации)
Пакеты прикладных программ.
Пакеты прикладных программ (ППП) служат программным инструментарием решения функциональных задач и являются самым многочисленным классом программных продуктов. В данный класс входят программные продукты, выполняющие обработку информации различных предметных областей.
Пакет прикладных программ – комплекс взаимосвязанных программ для решения задач определенного класса конкретной предметной области.
1. Общего назначения (универсальные)- программные продукты, предназначенные для автоматизации разработки и эксплуатации функциональных задач пользователя и информационных систем в целом. (текстовые редакторы, электронные таблицы, системы управления базами данных, интегрированные пакеты)
2. Методо-ориентированные — включают программные продукты, обеспечивающие независимо от предметной области и функций информационных систем математические, статистические и другие методы решения задач.
3. Проблемно-ориентированные — программные продукты, предназначенные для решения какой-либо задачи в конкретной функциональной области.
4. Интеллектуальные системы — реализуют отдельные функции интеллекта человека. Основными компонентами систем искусственного интеллекта являются базы знаний, интеллектуальный интерфейс с пользователем и программа формирования логических выводов.
Поддержка файловой системы
Файловые системы — неотъемлемая часть любой операционной системы. Они позволяют пользователям записывать и хранить файлы, получать доступ к данным, и, конечно же, пользоваться жесткими дисками.
Важное свойство файловых систем — поддержка журналирования. Журналируемая файловая система ведёт постоянный учёт всех операций записи на диск. Благодаря этому после сбоя электропитания файловая система всегда автоматически возвращается в рабочее состояние.
Поддержка файловой системы обеспечивается тем, что в составе всех современных операционных систем имеются специальные разделы ПО способные управлять процессом распределения дискового пространства для хранения данных, записывать в системной области диска в специальных таблицах размещения файлов (FAT-таблицах) данные о том, в каком месте диска хранятся тот или иной файл, представлять пользователю эти сведения в виде иерархической (файловой) структуры и обслуживать ее.
К функциям обслуживания файловой структуры относятся следующие операции, происходящие под управлением операционной системы:
· создание файлов и присвоение им имен
· создание каталогов (папок) и присвоение им имен
· переименование файлов и каталогов (папок);копирование и перемещение файлов между дисками компьютера и между каталогами (папками) одного диска;
· удаление файлов и каталогов (папок)
· навигация по файловой структуре с целью доступа к заданному файлу, каталогу (папке)
· управление атрибутами файлов.
Тестирование и отладка программ. Назначение и взаимосвязь. Методы тестирования. Примеры тестов для фрагмента программ.
Тестирование программы – процесс многократного выполнения программы с целью выявления в ней наличия ошибки.
Отладка – обнаружение, локализация и исправление ошибок программы.
Тест – это набор исходных данных с известными результатами.
Локализация — это нахождение места ошибки в программе.
· Основные тесты — должны проверять работоспособность программ для наиболее типичных данных
· Выраженные тесты – проверяют работоспособность программы в минимальном режиме
· Тесты граничных значений – проверяют на граничных значениях
· Аварийные тесты – проверяют реакцию программы на определенную аварийную ситуацию. В частности на ввод некорректных данных: деление на 0 и т.д.
Методы проектирования тестов:
· Метод «черного ящика» — соответствие входной и выходной информаций. ( по возможности перебрать все исходные данные).
· Метод «белого ящика» — учитывается структура алгоритма программы.
· Комбинирование – сначала программа рассматривается как «черный ящик», а потом запускается тест.
Локализация включает в себя:
· Определение сущности ошибки.
· Выявление фрагмента программы, в которой содержится ошибка.
· Установление конкретного места ошибки ( определяется методом ручной прокрутки: надо взять текст, а потом проанализировать работу программы)
Сортировка массива
Отсортировать массив- значит, переставить его элементы таким образом, чтобы для каждой пары выполнялось заданное условие упорядоченности.
Рассмотрим два способа сортировки массива:
1. Метод пузырька предлагает сравнивать каждый элемент с соседним. Если два элемента стоят неправильно, нарушая условие сортировки, то их меняют местами. Процесс перестановки продолжается до тех пор, пока все элементы не окажутся на своих местах. Тогда для всех пар элементов массива будет выполняться условие упорядоченности, и массив будет отсортирован.
2. Линейная сортировка массива ( методом поиска минимума)
При сортировке по возрастанию метод предлагает найти минимальный элемент в массиве и поставить его на нулевое место. А элемент с нулевого места переместить на место минимального элемента. После этого нулевой элемент массива гарантированно стоит на своем месте. Поэтому в дальнейшей сортировке он не участвует. На следующем шаге массив просматривается уже с первого элемента. В этой части находится свой минимум, который меняется местами с первым элементом. Теперь уже два элемента массива стоят на своих местах. На следующем шаге массив обрабатывается со второго элемента. Процесс продолжается до тех пор, пока в необработанной части массива не останутся два элемента. Среди них тоже находится минимальный. Он становится на предпоследнее место массива. А последний необработанный элемент автоматически попадает на последнее место в массиве. Теперь все элементы стоят на своих местах и процесс сортировки можно прекратить.
Помимо этих вариантов существует еще один частный случай линейной сортировки. Это минимаксная сортировка (максиминная). Согласно данному методу в необработанной части массива одновременно ищется максимальный и минимальный элементы, которые затем расставляются по своим метам в зависимости от направления сортировки. При этом необработанная часть массива сокращается одновременно с двух сторон.
Процедуры и функции. Сравнительная характеристика. Примеры использования.
Подпрограммы делятся на два класса: процедуры и функции.
Процедура – самостоятельная часть программного кода, имеющая имя и параметры, выполняющая некоторую последовательность действий и изменяющая значения некоторых своих параметров.
Функция – это самостоятельная часть кода, имеющая имя и вычисляющая на основе своих параметров (аргументов) некоторое значение, которое затем передается вызывающей программе.
| Функция | Процедура |
| Возвращает всегда только один результат | Возвращает любое количество результатов, вплоть до ни одного |
| Возвращает результат под именем функции | Возвращает результат через параметры |
| Вызывается внутри другого оператора ( специальной команды нет) | Вызывается с помощью специальной команды “Оператор вызова процедуры” |
| Имеет тип (аналогично переменной) | Не имеет типа |
Позиционные системы счисления. Перевод целых и дробных чисел из десятичной в двоичную систему счисления и обратно.
Позиционная система счисления— система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией.
Перевод целых чисел из 10 в 2 систему счисления и обратно
Необходимо последовательно делить х и получаемые частные на n (основание новой системы) до тех пор, пока не получится частное меньше n.
Запись: последнее частное и остатки от деления, записываемые в обратной последовательности.
Перевод из любой позиционной системы в десятичную выполняется, используя разложение по степеням основания.
Переводы дробных чисел из 10 в 2 систему счисления
Разложение числа по степеням основания
· Вначале переводится целая часть десятичной дроби в двоичную с.с.
· Затем, дробная часть десятичной дроби умножается на основание двоичной с.с.
· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной с.с.
· Алгоритм завершается, если дробная часть полученного произведения равна 0 или, если достигнута требуемая точность вычисления. В противном случае, вычисления продолжаются с предыдущего шага.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.