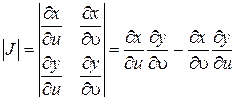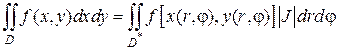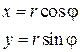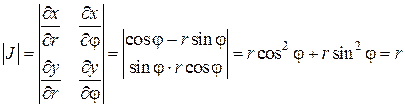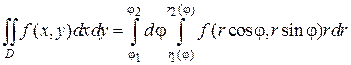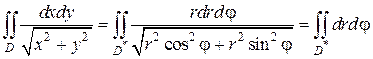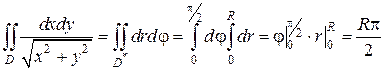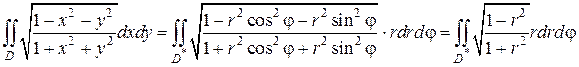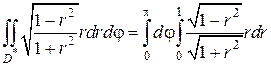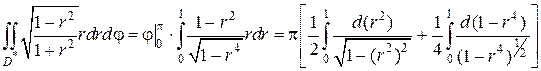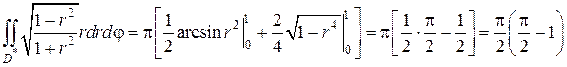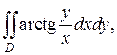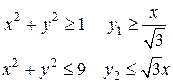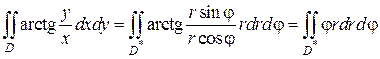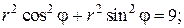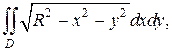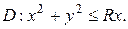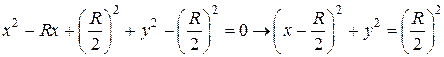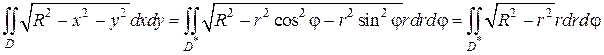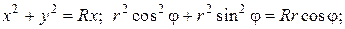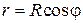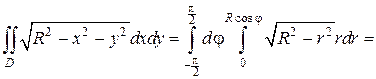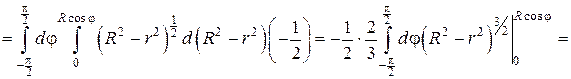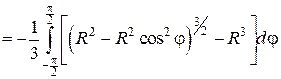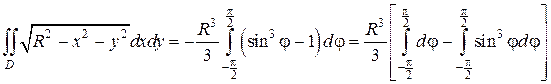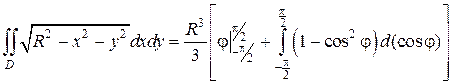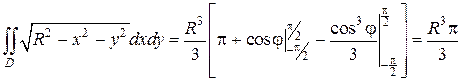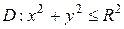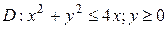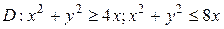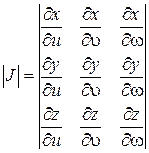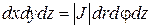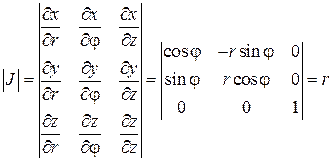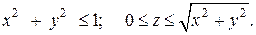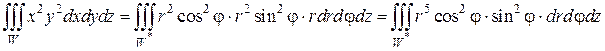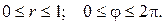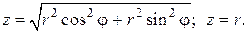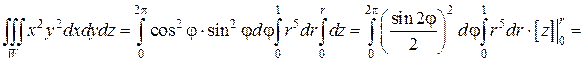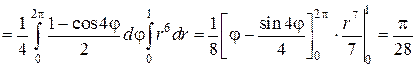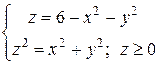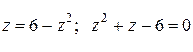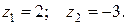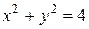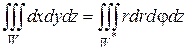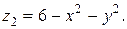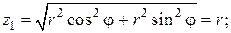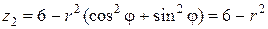Двойные интегралы в полярных координатах: теория и примеры
Что значит вычислить двойной интеграл в полярных координатах?
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый
Полюс O находится вне области интегрирования D .
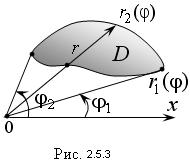
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Решения двойных интегралов в полярных координатах: примеры
Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 


Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 




Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности 
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности 




Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 



Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Двойной интеграл в полярной системе координат



Замена переменных интегрирования х и у в двойном интеграле, часто существенно упрощает его вычисление.
Пусть с помощью функций:
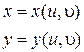
осуществляют переход от старых координат x, y к новым u, υ.
Эти функции должны быть непрерывными вместе со своими частными производными и однозначно решаться относительно u и υ. При этих условиях область D будет однозначно отображаться в область D * .
При переходе от декартовых к криволинейным координатам элемент площади dxdy преобразуется в элемент площади dudυ при этом они связаны соотношением:
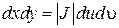
где 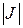
Таким образом, в общем случае замену переменных интегрирования в двойном интеграле осуществляют по формуле:
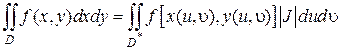
Из выражения (2.5.3) следует, что для того чтобы в двойном интеграле перейти к новым переменным интегрирования, нужно: переменные x и y заменить функциями (2.5.1), вместо элемента площади ds = dxdy подставить выражение 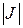
Перейдем в двойном интеграле от декартовых к полярным координатам по формуле (2.5.3), при этом за u примем полярный радиус r, а за υ – угол φ:
Функции x(r,φ) и y(r, φ) известны, они равны:
Найдем определитель Якоби:
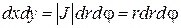
и двойной интеграл в полярной системе координат примет вид:
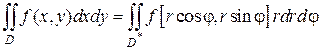
Чтобы вычислить полученный интеграл (2.5.5), следует перейти к двукратному интегрированию по новым переменным r и φ, а для этого нужно найти пределы их изменения в области D * .
Построение области D * в полярных координатах не обязательно. Если построена область D в декартовой системе координат, то пределы изменения полярного радиуса r и угла φ в новой системе отсчета легко определить по области D.
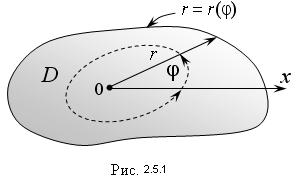
Например, пусть область D ограничена замкнутой кривой, а полюс лежит внутри кривой (рис. 2.5.1).
В этом случае нужно найти полярное уравнение ограничивающей линии r = r(φ).
Тогда угол φ внутри области будет изменяться от 0 до 2π, а полярный радиус r – от 0 до своих значений на кривой r = r(φ), т.е.:
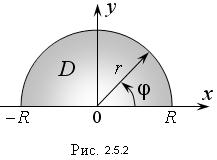
Если область D в декартовой системе отсчета есть полукруг радиуса R с центром в начале координат, расположенный в верхней полуплоскости (рис. 2.5.2), то значения полярного радиуса r и угла φ внутри D заключены в пределах 0 ≤ r ≤ R, 0 ≤ φ ≤ π,
следовательно:
И наконец может быть еще такой случай. Полюс лежит за пределами области D (Рис. 2.5.3), которая ограничена двумя линиями:
тогда
Приведем несколько примеров.
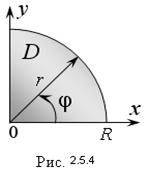
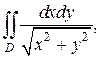
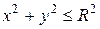
Решение. Построим область D в декартовой системе координат (рис. 2.5.4). В двойном интеграле перейдем к полярным координатам по формуле (2.5.5):
Полярный угол φ в области D изменяется от 0 до 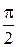
Пример 2. Вычислить двойной интеграл 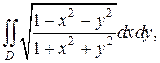
Решение. Перейдем к полярным координатам в двойном интеграле
Значения переменных φ и r заключены в пределах 0 ≤ φ ≤ π, 0 ≤ r ≤ 1, поэтому
Каждый из линейных интегралов в правой части равенства можно вычислить отдельно, так как пределы постоянны:
Находя первообразные и подставляя пределы окончательно получим:
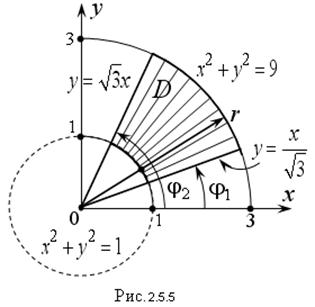
Пример 3. Вычислить двойной интеграл
где D есть часть кольца, определяемая неравенствами:
Решение. Построим область D (рис. 2.5.5). Вычисление данного интеграла в декартовой системе координат довольно громоздко, поэтому лучше преобразовать двойной интеграл к полярным координатам:
В области D полярный радиус r изменяется от 1 до 3, а полярный угол φ от 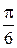
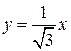
Примечание. Уравнения окружностей x 2 + y 2 = 1 и x 2 + y 2 = 9 в полярной системе представляют собой координатные линии вида r = 1 и r = 3 соответственно. В этом легко убедиться, если в данные уравнения вместо переменных x и y подставить их выражения через полярные координаты:
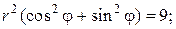
Уравнения прямых 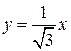
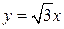
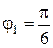
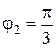
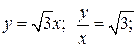
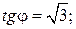
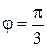
Пример 4. Вычислить двойной интеграл
где область интегрирования задана неравенством
Решение. Преобразуем уравнение 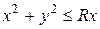
Следовательно, границей области D является окружность радиуса 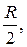
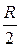
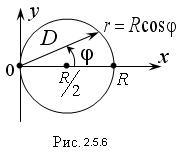
В данном случае также удобно перейти к полярным координатам:
Полярный угол φ будет изменяться от 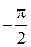
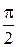
Полярный радиус r внутри области D изменяется от 0 до своих значений на линии r = Rcosφ (Рис. 2.5.6), т.е. пределы во внутреннем интеграле зависят от φ. Поэтому интегрируем сначала по r:
В последнем выражении вынесем за знак интеграла R 3 и учтем, что 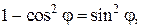
Вычисляя последние интегралы по переменной φ, окончательно получим:
Из приведенных примеров следует, что когда область интегрирования представляет собой круг, кольцо или часть круга и кольца с центром в начале координат, то при переходе к полярной системе, пределы у новых переменных φ и r становятся постоянными, а это значительно упрощает вычисления двойных интегралов.
Задачи для самостоятельного решения. Перейти к полярным координатам в двойном интеграле 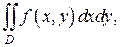
Расставить пределы для переменных r и j.
1.
2.
3.
4. Перейти к полярным координатам в интеграле 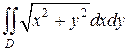
расставить пределы, если область D ограничена линиями:
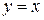
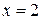
5. 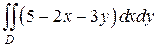
6. Вычислить 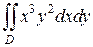
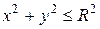
Практическое занятие 2.6. Тройной интеграл в цилиндрической и сферической системах координат
В общем случае замену переменных интегрирования в тройном интеграле осуществляют так же, как и в двойном.
Пусть функции:
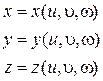
непрерывны вместе со своими частными производными и однозначно разрешаются относительно u, υ, ω. Тогда, с помощью этих функций область W в декартовой системе координат однозначно отображается в область W * в криволинейной системе координат.
При этом элементы dV и dV * в старой и новой системах будут связаны соотношением:
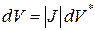
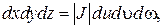
В результате тройной интеграл преобразуется по формуле:
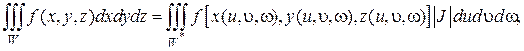
а его вычисление сводят к трехкратному интегрированию по переменным u, υ, ω. Примерами криволинейных систем в пространстве могут служить цилиндрическая и сферическая системы координат. Перейдем к их рассмотрению.
Тройной интеграл в цилиндрических координатах
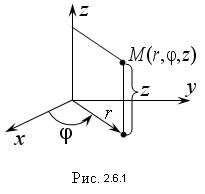
Положение точки в пространстве в цилиндрической системе координат однозначно задают тремя числами φ, r, z.
Цилиндрические координаты точки получают путем добавления к ее полярным координатам аппликаты z (рис. 2.6.1). Цилиндрические и декартовые координаты точки связаны между собой соотношениями:
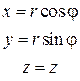
Перейдем в тройном интеграле от декартовых к цилиндрическим координатам. Элемент объема dV преобразуется по формуле
Найдем определитель Якоби:
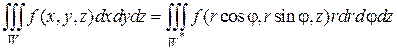
Далее, нужно перейти к трем линейным интегралам по переменным r,φ,z. Пределы изменения новых переменных расставляют по виду области W. Так же как и в двойном интеграле строить область W * не обязательно. Покажем это на примере.
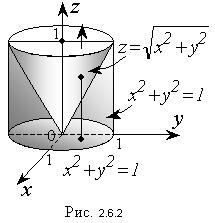
Пример 1. Вычислить тройной интеграл 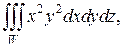
Решение. Область, по которой нужно вычислить тройной интеграл, заключена внутри цилиндра 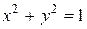
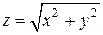
Цилиндрическая поверхность и конус пересекаются по линии 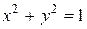
Найдем пределы изменения r,φ,z. Проекция W на плоскость xОy – есть круг, ограниченный окружностью 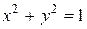
Для определения границ изменения переменной z, проведем прямые, параллельные оси Oz. Эти прямые будут входить в область W на плоскости
z = 0 и выходить из нее на конической поверхности 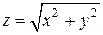
Таким образом, переменная z в области W изменяется от 0 до своих значений на конусе z = r. Переходя к трехкратному интегрированию по переменным r, φ и z, получим:
В данном примере проекцией W на плоскость xOy был круг с центром в начале координат, поэтому при переходе к цилиндрическим координатам пределы у переменных r и φ были постоянными. Это упростило вычисление тройного интеграла.
Пример 2. Вычислить тройной интеграл 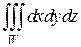
Решение. Область ограничена двумя поверхностями: снизу – конусом 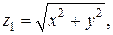
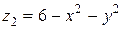
Их линией пересечения является окружность. Найдем ее уравнение из условия 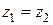
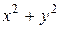
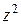
Корни полученного квадратного уравнения раны
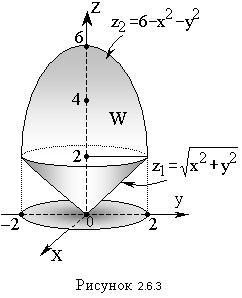
Так как область W проектируется на плоскость xOy в круг с радиусом R = 2, и центром в начале координат, в тройном интеграле перейдем к цилиндрическим координатам:
Внутри области W полярный угол φ изменяется от 0 до 2π, а полярный радиус r – от 0 до 2. Значения переменной z заключены между двумя поверхностями 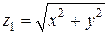
Найдем их уравнения в цилиндрической системе отсчета
Расставляя пределы изменения для переменных φ, r и z и переходя к трехкратному интегрированию, получим