Перевод иконок в статграфикс

Работа с пакетом STATGRAPHICS Plus 5.0: Учебно-методическое пособие

Страницы работы

Содержание работы

Работа с пакетом STATGRAPHICSPlus 5.0

Для того чтобы начать работу с пакетом STATGRAPHICS Plus 5.0 необходимо:

1. Нажать кнопку «Пуск» и выбрать раздел «Программы».

2. В разделе «Программы» выбрать «STATGRAPHICS Plus 5.0».

3. В разделе «STATGRAPHICS Plus 5.0» выбрать «Sgwin».

1. Создание файла переменных.

1.1 Для ввода данных выберите окно «untitled».

1.2 В открывшемся окне введите элементы одной или нескольких выборок в столбик (целая часть числа от дробной отделяется запятой).

1.3 Для того, чтобы дать название выборке подведите курсор к заглавию столбца «Col» и нажмите левую клавишу мыши.

1.4 После выделения черным цветом указанного столбца нажмите правую клавишу мыши.

1.5 В открывшемся окне выбрать «Modify Column».

1.6 В открывшемся окне «Modify Column» в поле «Name» вместо «Col» наберите свое название выборки и нажмите «Ok».

1.7 Для записи переменных на диск в главном меню выберите «File».

1.8 В подменю выберите «Save».

1.9 В следующем подменю выберите «Save Data File».

1.10 В открывшемся окне «Save Data File As» в поле «Папка» выберите диск на который желаете записать фаил.

1.11 В поле «Имя файла» дайте имя своему файлу.

1.12 В поле «Тип файла» выберите «SG PLUS Files (*.sf 3;*.sf) и нажмите «Сохранить».

2. Вычисление оценок числовых характеристик.

2.1 В главном меню выберите «Describe».

2.2 В подменю выберите «Numeric Data».

2.3 В следующем подменю выберите «One-Variable Analysis».

2.4 В открывшемся окне «One-Variable Analysis» подведите курсор к той выборке («Col») которую желаете исследовать и выделите ее нажав левую клавишу мыши.

2.5 Нажмите клавишу «Data», а затем «Ok».

2.6 В открывшемся окне «One-Variable Analysis Col» нажмите вторую слева желтую иконку.

2.7 В открывшемся окне «Tabular Options» с помощью левой клавиши мыши поставьте галочку в поле «Summary Statistics», а галочки в других полях этой же клавишей уберите.

2.8 На левой стороне экрана появится таблица с результатами вычислений.

2.9 Для вычисления дополнительных характеристик нажмите правую клавишу мыши, когда курсор находится на левой стороне экрана.

2.10 В подменю выберите «Pane Options».

2.11 В открывшемся окне «Summary Statistics Options» поставьте галочки в полях тех характеристик, которые необходимо вычислить и нажмите «Ok».

Перевод английских терминов приводится ниже.

Count Объем выборки

Geometric mean Геометрическое среднее

Std. Deviation Стандартное отклонение

Std. Error Стандартная ошибка

Minimum Минимальное значение выборки

Maximum Максимальное значение выборки

Range Размах выборки

Lower quartile Нижняя квартиль

Upper quartile Верхняя квартиль

Interquar. range Интерквартильная широта распределения

Skewness Коэффициент асимметрии

Std. skewness Отклонение коэффициента асимметрии от канонического значения

Kurtosis Коэффициент эксцесса

Std. kurtosis Отклонение коэффициента эксцесса от канонического значения

Coeff. of Variation Коэффициент вариации

Sum Сумма элементов выборки

2.12 Для построения гистограммы относительных частот в окне «One-Variable Analysis Col» нажмите третью слева синюю иконку.

2.13 В открывшемся окне «Graphical Options» поставьте галочку в поле «Frequeney Histogram», а остальные галочки уберите и нажмите «Ok».

2.14 На правой стороне экрана появится гистограмма относительных частот.

2.15 Для вывода результатов на печать подготовьте принтер и в главном меню выберите «File».

2.16 В подменю выберите «Print».

2.17 В открывшемся окне «Print Analysis» в разделе «Print Range» выберите тип распечатки:

All Panes Все окна

Visible Panes Видимые окна

All Text Panes Текстовые окна

All Graphics Panes Графические окна

2.18 В главном меню выберите «File».

2.19 В подменю выберите «Print Setup».

2.20 В открывшемся окне «Настройка принтера» в поле «Имя» выберите необходимый принтер и нажмите «Ok».

Подбор закона распределения

ЛМ – нажать левую клавишу мыши;

ЛМ2 – дважды нажать левую клавишу мыши;

ПМ – нажать правую клавишу мыши.

В данном разделе описана методика проверки согласования с экспериментальными данными гипотезы о виде закона распределения изучаемой случайной величины, заданной выборкой.

Для выполнения этих процедур необходимо записать выборку значений переменой в файл и определиться с выбором уровня значимости a.

1. Открыть файл, в котором записана требуемая переменная. Для этого:

– На панели управления выбрать символ «», ЛМ,

– В главном меню выбрать раздел File, ЛМ, затем – Open, ЛМ, затем – Open Data File, ЛМ,

– Нажать комбинацию клавиш + .

В появившемся окне «Open Data File» с помощью курсора («мыши») выбрать имя нужного файла, нажать кнопку «Ok».

Источник

Работа с пакетом STATGRAPHICS Plus 5.0: Учебно-методическое пособие , страница 2

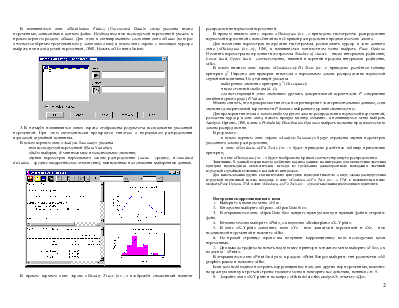
2. В главном меню выбрать раздел Describe, ЛМ, в появившемся окне – Distributions, ЛМ, затем – Distribution Fitting (Uncensored Data), ЛМ.

В появившемся окне «Distribution Fitting (Uncensored Data)» слева указаны имена переменных, записанных в данном файле. Необходимо имя исследуемой переменной указать в правом верхнем разделе «Data». Для этого в активированном состоянии окна «Data» (которое отмечается чёрным треугольником у заголовка окна) в левом окне экрана с помощью курсора выбрать имя исследуемой переменной, ЛМ2. Нажать «Ok» или .

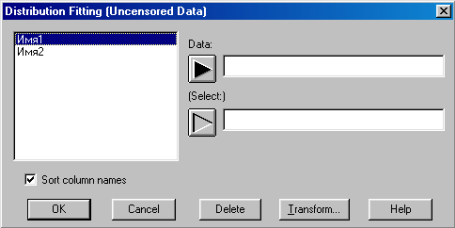
3. В четырёх появившихся окнах экрана отображены результаты исследования указанной переменной. При этом автоматически проверяется гипотеза о нормальном распределении изучаемой случайной величины.

В левом верхнем окне «Analysis Summary» указаны

– имя исследуемой переменной (Data Variable);

– объём выборки, её минимальное и максимальное значения;

– оценки параметров нормального закона распределения (mean – среднее, и standard deviation – среднее квадратическое отклонение), вычисленные на основании выборочных данных.

В правом верхнем окне экрана «Density Trace for…» изображён сглаженный полигон распределения изучаемой переменной.

В правом нижнем окне экрана «Histogram for…» приведена гистограмма распределения изучаемой переменной с нанесённой на неё кривой распределения предполагаемого закона.

Для изменения параметров построения гистограммы, расположить курсор в зоне данного окна («Histogram for…»), ПМ, в появившемся контекстном меню выбрать Pane Options. Изменить параметры построения гистограммы: Number of classes – число интервалов разбиения; Lower limit, Upper limit – соответственно, нижний и верхний пределы интервалов разбиения, «Ok».

В левом нижнем окне экрана «Goodness-of-Fit Tests for…» приведена расчётная таблица критерия c 2 Пирсона для проверки гипотезы о нормальном законе распределения изучаемой случайной величины. Под таблицей указаны:

– выборочное значение критерия c 2 (Chi-square);

– число степеней свободы (d. f.);

– соответствующий этим значениям уровень доверительной вероятности P совершения ошибки первого рода (P-Value).

Можно считать, что проверяемая гипотеза не противоречит экспериментальным данным, если значение доверительной вероятности P больше выбранного уровня значимости a.

Для проверки гипотезы о каком-любом другом законе распределения изучаемой переменной, разместив курсор в зоне окна, нажать правую кнопку «мыши», в появившемся меню выбрать Analysis Options, ЛМ, в окне «Probability Distribution Options» выбрать название предполагаемого закона распределения.

– в левом верхнем окне экрана «Analysis Summary» будут отражены оценки параметров указанного закона распределения;

– в окне «Goodness-of-Fit Tests for…» будет приведена расчётная таблица применения критерия;

– в окне «Histogram for…» будет изображена кривая соответствующего распределения.

Замечание. В данной версии пакета разбиение массива данных на интервалы для вычисления значения критерия производится автоматически, исходя из требования равновероятного попадания значений изучаемой случайной величины в каждый из интервалов.

Для использования других статистических критериев проверки гипотезы о виде закона распределения изучаемой переменной нужно, находясь в окне «Goodness-of-Fit Tests for…», ПМ, в появившемся меню выбрать Pane Options, ЛМ, в окне «Goodness-of-Fit Tests for…» указать названия необходимых критериев.

Построение корреляционного поля

1. Выберите в главном меню «File».

2. В подменю выберите «Open» — «Open Data file».

3. В открывшемся окне «Open Data file» найдите нужную папку и нужный файл и откройте файл.

4. В главном меню выберите «Plot», а в подменю «Scatterplots» «X‑Y plot».

5. В окне «X‑Y plot» заполните поля «Y» – имя зависимой переменной и «X» – имя независимой переменной и нажмите «Ok».

6. На правой странице экрана вы получили корреляционное поле исследуемых вами переменных.

7. Для вывода графика на печать подготовьте принтер и в главном меню выберите «File», а в подменю – «Print».

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Компонентный анализ в среде StatGraphics

Для проведения расчетов в среде StatGraphics нужно занести данные на электронный лист, например, скопировать через буфер обмена с листа Excel. Лучший вариант – сохранение данных в формате листа Excel ранних версий. Рассмотрим ключевые этапы работы для примера с морфологической изменчивостью гадюк.

Открыть в среде StatGraphics файл следует командой меню или кнопкой Open Data File.

Чтобы имена переменных, назначенных в Excel, автоматически становились именами столбцов, они должны даваться латиницей; в окошке запроса отметить, что имена переменных в первом ряду есть.

Результаты экспорта данных можно посмотреть в окне данных, специально распахнув окно иконки, лежащей на сером поле слева в нижнем углу.

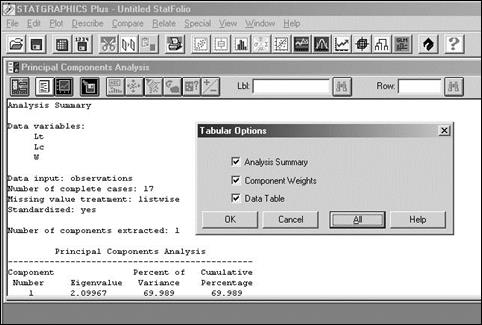
Запустить программу компонентного анализа можно только командой меню Special\ Multivariate Methods\ Principal Components.

Выбрав мышкой имена нужных переменных, кнопкой Data: их нужно скопировать в правое окно, ОК. Для дальнейшей идентификации объектов, их метки следует поместить в окно Point Labels:.

В появившемся окне Principal Component Analysis четыре кнопки играют важную роль. Первая слева кнопка Input Dialog позволяет вернуться на предыдущий шаг и переопределить список анализируемых переменных. Кнопка Tabular Options обеспечивает доступ ко всем результатам анализа (All, OK). Окно Analysis Summary выводит значения дисперсий главных компонент, окно Table of Component Weights дает значения факторных нагрузок, в окно Table of Principal Components выведены значения главных компонент.

Кнопка Graphical Options раскрывает окна с графическими иллюстрациями (All, OK).

Все окно результатов компонентного анализа предстает в виде десяти небольших окошек; распахнуть любое из них позволяет двойной клик левой кнопкой мыши.

Полнота результатов вычислений во многом определяется установками в окне Principal Components Options, которое вызывается командой контекстного меню Analysis options… (правый клик на любом окне анализа). Минимально необходимый объем информации появляется, если в блоке Extract by … Number of Components задать число 2 (т. е. выводить результаты для двух компонент); кроме того, можно задать иное минимальное значение дисперсии главной компоненты (Eigenvalue), чем принятое по умолчанию значение 1. В результате на графиках и в таблицах будут отображаться данные по компонентам, дисперсия которых превышает заданный уровень.

Диаграмма факторных нагрузок (Plot of Component Weights) копирует таблицу Table of Component Weights и призвана наглядно представить степень коррелированности соответствующих признаков.

График Scree Plot отражает изменение дисперсий компонент и (пунктиром) минимальный уровень значимых компонент.

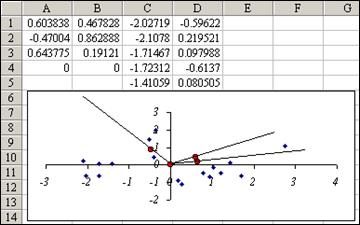
Наиболее интересна диаграмма Scatterplot, где представлена ординация объектов в осях компонент,

а также Biplot, где к диаграмме Scatterplot добавлена диаграмма Plot of Component Weights в форме лучей.

Каждый из этих лучей построен по двум опорным точкам: в месте пересечения осей компонент (0,0) и в точке с координатами факторных нагрузок двух первых компонент (a_1j,a_2j) (здесь j – номер соответствующего признака). Это возможно потому, что и компоненты, и факторные нагрузки есть безразмерные признаки. Биплот наглядно показывает направления изменчивости данных, за которые ответственны определенные признаки. По промерам гадюк видно, что первое направление изменчивости (выявленное первой главной компонентой) определяет отличие особей по массе (W) и длине тела (Lt), а второе (вторая компонента) связано в основном с отличиями по длине хвоста (Lc).

Результаты расчетов можно поместить на электронный лист (с помощью кнопки Save results, поставив галочки в нужных окошках), через буфер обмена скопировать на лист Excel, и воспользоваться его богатыми графическими возможностями.

В частности, чтобы понять принцип построения биплота, следует объединить (копированием) две точечные диаграммы, построенные раздельно по значениям главных компонент и факторных нагрузок, соединив лучами точки нагрузок с пересечением осей.

Имитационное моделирование в среде Excel

Вообще говоря, любая мысль об окружающем мире есть его модель. Имитационная модель – это компьютерная программа, которая служит для количественного отображения поведения реальных объектов в разных условиях. Смысл построения имитационных моделей состоит, во-первых, в том, чтобы установить (выразить уравнением) количественные закономерности протекания явлений природы, во-вторых, – оценить модельные параметры (коэффициентов пропорциональности между переменными уравнений). Параметры моделей часто имеют биологический смысл, поскольку выражают существо отношений между характеристиками объектов исследования.

Моделирование пока не столь широко распространено, как того требуют сложные задачи современной биологии, особенно экологии. На наш взгляд, одним из препятствий этому служит распространенное мнение, что «полноценными» могут быть лишь дающие прогноз аналитические модели; сопряженные с этим сложности построения системы дифференциальных уравнений и их решения оказываются серьезным препятствием для большинства биологов. Однако изучаемые экологические явления сначала нужно понять, дать им объяснение, а уж затем, при необходимости, и прогнозировать.

Мы предлагаем давать количественное объяснение с помощью имитационного моделирования – составлять модели, основанные на простейших (линейных) алгебраических уравнениях, и определять значения их параметров посредством внешних процедур «оптимизации».

Вместо составления и решения дифференциальных уравнений предлагается составлять программы и настраивать параметры имитационных моделей. Обе эти проблемы оптимально решаются в среде пакета Microsoft Excel.

Способ построения моделей на листе Excel отличается от традиционных способов программирования (алгоритмического, структурного или объектного) – это табличное программирование. На листе Excel модель предстает в всех своих деталях, как таблица, ячейки которой заполнены формулами, имитирующими либо выборку вариант (статические модели), либо ход процесса (динамические модели). Каждая ячейка содержит формулу, которая вычисляет соответствующее «модельное» значение варианты или характеристику системы на очередном временнóм шагу. Поскольку «объяснительные» значения модельных переменных должны более или менее совпадать с реальными наблюдениями, организуется процедура поиска таких (оптимальных) значений модельных параметров, которые делают отличия между моделью и реальностью наименьшими, минимизируют «функцию отличий», или «функцию невязки». Эта процедура оптимизации выполняется с помощью отдельной программы «Поиск решения», встроенной в пакет Excel. (Ответственное отношение к моделированию требует понимания существа процедуры настройки! [см.: Коросов, 2002]).

Помимо программирования самой модели и настройки ее параметров требуется доказать значимость модельных параметров, адекватность модели. Для решения этой задачи на листе Excel приходится конструировать целую имитационную систему, состоящую из следующих компонентов:

· блок исходных данных, зачастую состоящий из массива независимых и зависимых переменных;

· блок расчета модельных данных, собственно имитационная модель, состоящая из уравнений; осуществляет расчет явных переменных и скрытых переменных;

· блок параметров, участвующих в расчете модельных данных и изменяемых в процессе настройки;

· блок расчета отличий реальных и расчетных значений переменных;

· значение суммы отличий между моделью и реальностью (значение функции невязки); оно минимизируется в процессе настройки;

· блок процедуры настройки (программа «Поиск решения»);

· блок графического представления результатов;

· блок статистической оценки результатов.

В результате несложных действий мы получаем очень гибкий инструмент описания действительности. В потенциях имитационной модели стать сложной и детализированной или, напротив, простой и обобщающей, выражающей законы, управляющие миром.

Источник