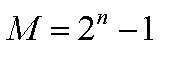Перевод информации в двоичный код

Двоичный код.

Двоичный код — это подача информации путем сочетания символов 0 или 1. Порою бывает очень сложно понять принцип кодирования информации в виде этих двух чисел, однако мы постараемся все подробно разъяснить.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.

Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.

На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.

Перевод натурального числа десятичной системы счисления в двоичную систему.

Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:

1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.

2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.

3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.

4. В этот момент считается, что двоичный код готов.

Для примера переведем в двоичную систему число 7:

1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.

2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.

3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.

4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.

Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.

Перевод числа двоичной системы в десятичную.

Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.

Немного из истории двоичной системы счисления.

Принято считать, что впервые двоичную систему предложил Готфрид Вильгельм Лейбниц, который считал систему полезной в сложных математических вычислениях и науке. Но по неким данным, до его предложения о двоичной системе счисления, в Китае появилась настенная надпись, которая расшифровывалась при использовании двоичного кода. На надписи были изображены длинные и короткие палочки. Предполагая, что длинная это 1, а короткая палочка — 0, есть доля вероятности, что в Китае идея двоичного кода существовала многим ранее его официального открытия. Расшифровка кода определила там только простое натуральное число, однако это факт, который им и остается.

Источник

Перевод информации в двоичный код – что это такое, его виды, расшифровка

Всем известна такая способность компьютеров, как вычисление больших групп данных практически за считанные секунды. Однако не каждый знает, что это умение электронных машин зависит от наличия тока и напряжения.

Что такое двоичный код?

Как же компьютеру удаётся быстро обрабатывать огромные объёмы информации? Помогает ему в этом двоичная система исчисления. Данные, поступающие в это умное устройство, выглядят как единицы и нули. Каждой единице и каждому нулю соответствует определённое состояние электропровода:

• 1 — высокое напряжение.
• 0 — низкое.

Или же для единиц — наличие напряжения, а для нулей — отсутствие.

Основой двоичной системы исчисления являются двоичные коды. Что такое двоичный код?

Процесс, когда данные преобразуются в нули и единицы, называют «двоичная конверсия», а окончательное их обозначение — «двоичный код».

Разрядность двоичного кода

Все двоичные числа являются совокупностью битов, то есть, единиц и нулей, а каждый бит является одним разрядом или одной позицией в двоичном числе. Часто в задачах по информатике встречается вопрос, какое количество информации несёт тот или иной двоичный код. Следует знать, что в каждой цифре двоичного кода содержится количество информации, которое равно одному биту.

Что такое разрядность двоичного кода? Если смотреть с точки зрения арифметики, то под разрядностью понимается место, которое занимает цифра при записи чисел. Тогда под разрядностью двоичного кода подразумевается количество мест знаков (разрядов) или количество битов, которые заранее отведены для того, чтобы записать число.

Расшифровка двоичного кода

Как же расшифровать двоичный код? Десятичное обозначение основано на десятичной системе исчисления, которую обычно используют в повседневной жизни и числовые значения здесь представлены в виде десяти цифр от нуля до девяти. Каждое из мест в числах в десять раз больше по ценности, чем место, находящееся справа. Для представления числа больше 9 в десятичной системе используется ноль, который ставится справа. А единица расположена слева на следующем, более ценном месте.

Подобным образом устроена и двоичная система, в которой используют только две цифры — ноль и единицу. Места слева ценнее в два раза, чем места справа. Так, для двоичного кода характерно, что одноместными числами могут быть только 0 и 1, а для любых чисел больше единицы требуется уже 2 места.

После 0 и 1 следуют такие двоичные числа:

В двоичной системе 100 — это эквивалент цифры 4 десятичной системы. Таким образом, любое число можно выразить в виде двоичного кода, но оно будет занимать больше места. Также, закрепив за каждой буквой алфавита определённые двоичные числа, можно осуществить перевод в двоичный код любое слово.

Видео о переводе чисел в двоичный код

К примеру, для передачи сообщения по цифровому каналу связи, его кодируют, то есть, сопоставляют каждый символ исходного сообщения с некоторым кодом (кодовым словом). Для этого используются двоичные коды — последовательность единиц и нулей.

Например, чтобы закодировать слово «мама» выбирается следующий код:

Закодированные буквы соединятся в одну битовую строчку и будут переданы по сети в таком виде:

МАМА МЫЛА ЛАМУ → 0010011100010111010010

После того как эта строка будет доставлена к пункту назначения, следует решить проблему восстановления исходного сообщения. Так, получив сообщение «001001», его раскодирование можно осуществить несколькими способами. К примеру, предположив, что оно состоит только из букв Л (код 0) и А (код 1), получится:

Это значит, что вышеприведённый код не декодируется однозначно. Однозначно декодируемые коды — это такие коды, в которых любые кодовые сообщения расшифровываются только одним способом.

Данная проблема решается путём правильного разбития битовой цепочки на отдельно закодированные слова. Это можно сделать, к примеру, с использованием равномерного кода, длина слов в котором всегда одинакова. К примеру, данная фраза состоит из шести символов, а это значит, что можно применить трехбитный код.

Например, если закодировать вышеприведённую фразу с помощью такого кода:

• М — 000.
• А — 001.
• Ы — 010.
• Л — 011.
• Пробел — 101, то получится следующее:

МАМА МЫЛА ЛАМУ → 000001000001101000010011001101011001000100

Это сообщение имеет длину 42 бита. Несмотря на то что оно длиннее, чем первое, состоящее всего из 22 бит, его значительно легче разобрать на отдельные слова для раскодирования:

000 001 000 001 101 000 010 011 001 101 011 001 000 100

М А М А _ М Ы Л А _ Л А М У

Хотя такой равномерный код нельзя назвать экономичным, зато его можно однозначно декодировать.

Видео о переводе букв в двоичный код

Неравномерные коды

Неравномерный двоичный код — что это такое? Его иногда применяют для сокращения длины сообщений. В неравномерном коде кодовое слово, соответствующее определённому символу в алфавите, может отличаться по длине от других слов.

Например, если использовать для кодирования «Мама мыла ламу» такой код:

• М — 01.
• А — 00.
• Ы — 1011
• Л — 100.
• У — 1010.
• Пробел — 11, то получится:

МАМА МЫЛА ЛАМУ → 0100010011011011100001110000011010

Данное сообщение состоит из 34 бит. Эту битовую цепочку можно декодировать однозначно, поскольку в первой букве — М, имеющей код 01, код является уникальным, ведь другие кодовые слова не начинаются с 01. Таким же образом можно определить вторую букву — А. Свойство, когда кодовые слова не совпадают с началом других кодовых слов, называют условием Фано, а коды, декодируемые с помощью свойства Фано, называются префиксными.

Префиксные коды отличаются важным практическим значением — с их помощью декодируются символы получаемых сообщений по мере их поступления, не ожидая, когда всё сообщение придёт к получателю.

Виды двоичных кодов

Для представления целых чисел существуют следующие виды двоичных кодов:

Отрицательные числа могут быть представлены только в знаковом виде. Хранение целых чисел в компьютере осуществляется в формате с фиксированной запятой.

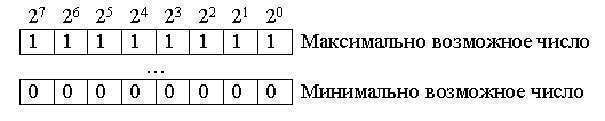
В целых беззнаковых двоичных кодах все двоичные разряды представлены в степени цифры 2:

Значение минимально возможного числа равняется нулю, а максимальное определяется по формуле:

С помощью этих двух чисел определяется диапазон чисел, представленных в виде двоичного кода.

• Если представлено восьмиразрядное беззнаковое целое число, то диапазон чисел записывается с помощью кода: 0…255.
• Если представлен шестнадцатиразрядный код — 0…65535.

В восьмиразрядных процессорах такие числа хранятся в двух ячейках памяти, которые расположены в соседних адресах. Работа с подобными числами осуществляется с помощью специальных команд.

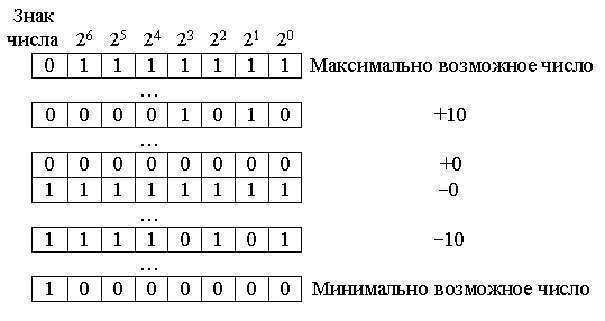
В прямых целых знаковых кодах представление знака числа осуществляется с помощью старшего разряда в слове. Для прямого знакового кода для обозначения знака «+» используется ноль, а знака «-» — единица. При введении знакового разряда произойдёт смещение диапазона чисел в сторону отрицательных значений.

• Двоичное восьмиразрядное знаковое целое число записывается с помощью такого диапазона: -127…+127.
• Шестнадцатиразрядный код будет записан в диапазоне: -32767…+32767.

В восьмиразрядных процессорах такие числа хранятся также в двух ячейках памяти, адреса которых расположены рядом.

В качестве недостатка этого кода можно назвать необходимость раздельной обработки знакового и цифрового разрядов. Программы, работающие в таких алгоритмах, являются довольно сложными. Для того чтобы выделить и изменить знаковый разряд, придётся применить метод маскирования разрядов, что приводит к увеличению размера программы и уменьшению её быстродействия. Для предотвращения возникновения различий в алгоритме обработки цифрового и знакового разрядов используются обратные двоичные коды.

Отличие знаковых обратных двоичных кодов от прямых заключается в образовании отрицательных чисел с помощью инвертирования всех разрядов чисел. Однако при этом цифровой и знаковый разряды не имеют различий. Такие коды позволяют значительно упростить алгоритм работы.

Но, несмотря на это, работа с обратными кодами требует специального алгоритма для того, чтобы распознавать знаки, вычислять абсолютные значения чисел, восстанавливать знак результата числа. Также прямой обратный код числа требует для запоминания нуля использовать два кода в то время, когда известно, что ноль является положительным числом, и отрицательным он быть не может никогда.

А Вы знаете, что такое двоичный код и как его расшифровать? Помогли ли Вам в жизни эти знания? Расскажите об этом в комментариях.

Источник

Перевод текста в цифровой код.

Давайте разберемся как же все таки переводить тексты в цифровой код? Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.

Кодирование текста.

По теории ЭВМ любой текст состоит из отдельных символов. К этим символам относятся: буквы, цифры, строчные знаки препинания, специальные символы ( «»,№, (), и т.д.), к ним, так же, относятся пробелы между словами.

Необходимый багаж знаний. Множество символов, при помощи которых записываю текст, называется АЛФАВИТОМ.

Число взятых в алфавите символов, представляет его мощность.

Количество информации можно определить по формуле : N = 2b

• N – та самая мощность ( множество символов),
• b – Бит ( вес взятого символа).

Алфавит, в котором будет 256 может вместить в себя практически все нужные символы. Такие алфавиты называют ДОСТАТОЧНЫМИ.

Если взять алфавит мощностью 256, и иметь в виду что 256 = 28

• 8 бит всегда называют 1 байт:
• 1 байт = 8 бит.

Если перевести каждый символ в двоичный код, то этот код компьютерного текста будет занимать 1 байт.

Как текстовая информация может выглядеть в памяти компьютера?

Любой текст набирают на клавиатуре, на клавишах клавиатуры, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111.

Поскольку, байт – это самая маленькая адресуемая частица памяти, и память обращена к каждому символу отдельно – удобство такого кодирование очевидно. Однако, 256 символов – это очень удобное количество для любой символьной информации.

Естественно, встал вопрос: Какой конкретно восьми разрядный код принадлежит каждому символу? И как осуществить перевод текста в цифровой код?

Этот процесс условный, и мы вправе придумать различные способы для кодировки символов. Каждый символ алфавита имеет свой номер от 0 до 255. И каждому номеру присвоен код от 00000000 до 11111111.

Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для различных типов ЭВМ используют разные таблицы для кодировки.

ASCII(или Аски), стала международным стандартом для персональных компьютеров. Таблица имеет две части.

Таблица кода символов ASCII.

Первая половина для таблицы ASCII. (Именно первая половина, стала стандартом.)

Соблюдение лексикографического порядка, то есть, в таблице буквы (Строчные и прописные) указаны в строгом алфавитном порядке, а цифры по возрастанию, называют принципом последовального кодирования алфавита.

Для русского алфавита тоже соблюдают принцип последовательного кодирования.

Сейчас, в наше время используют целых пять систем кодировок русского алфавита(КОИ8-Р, Windows. MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид.

Одним из первых стандартов для кодирования русского алфавита на персональных компьютерах считают КОИ8(«Код обмена информацией, 8-битный»). Данная кодировка использовалась в середине семидесятых годов на серии компьютеров ЕС ЭВМ, а со средины восьмидесятых, её начинают использовать в первых переведенных на русский язык операционных системах UNIX.

С начала девяностых годов, так называемого, времени, когда господствовала операционная система MS DOS, появляется система кодирования CP866 («CP» означает «Code Page», «кодовая страница»).

Гигант компьютерных фирм APPLE, со своей инновационной системой, под упралением которой они и работали (Mac OS), начинают использовать собственную систему для кодирования алфавита МАС.

Международная организация стандартизации (International Standards Organization, ISO)назначает стандартом для русского языка еще одну систему для кодирования алфавита, которая называется ISO 8859-5.

А самая распространенная, в наши дни, система для кодирования алфавита, придумана в Microsoft Windows, и называется CP1251.

С второй половины девяностых годов, была решена проблема стандарта перевода текста в цифровой код для русского языка и не только, введением в стандарт системы, под названием Unicode. Она представлена шестнадцатиразрядной кодировкой, это означает, что на каждый символ отводится ровно по два байта оперативной памяти. Само собой, при такой кодировке, затраты памяти увеличены в два раза. Однако, такая кодовая система позволяет переводить в электронный код до 65536 символов.

Специфика стандартной системы Unicode, является включением в себя абсолютно любого алфавита, будь он существующим, вымершим, выдуманным. В конечном счете, абсолютно любой алфавит, в добавок к этом, система Unicode, включает в себя уйму математических, химических, музыкальных и общих символов.

Давайте с помощью таблицы ASCII посмотрим, как может выглядеть слово в памяти вашего компьютера.

Очень часто случается так, что ваш текст, который написан буквами из русского алфавита, не читается, это обусловлено различием систем кодирования алфавита на компьютерах. Это очень распространенная проблема, которая довольно часто обнаруживается.

Источник