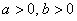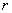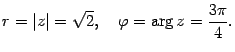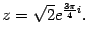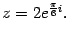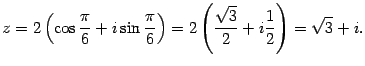Перевод комплексного числа в экспоненциальную форму

Перевод комплексного числа в экспоненциальную форму

Понятия комплексные или мнимые числа впервые начали применяться при решении квадратных уравнений. Когда дискриминант получался меньше нуля (D Онлайн калькулятор комплексных чисел

Программа выполняет вычисления c комплексными числами, представленными в алгебраической или показательной форме, а так же рациональными числами.

Сложение и вычитание комплексных чисел необходимо осуществлять в алгебраической форме, если число представлено в иной форме, нужно перевести его в алгебраическую, воспользовавшись калькулятором, или же вручную по формулам ниже:

Умножение и деление комплексных чисел возможно реализовать как в алгебраической, так и в показательной формах. Но намного практичней осуществлять действие в показательной форме, этот способ займет намного меньше времени при расчете, например, токов короткого замыкания.

Сложение сопряженных чисел:

При делении комплексных чисел в алгебраической форме необходимо избавиться от мнимой составляющей в знаменателе. Для этого числитель и знаменатель домножают на число, сопряженное знаменателю.

Перевод чисел из алгебраической формы в показательную и наоборот возможно осуществить с помощью калькулятора для комплексных чисел, который Вы можете скачать по ссылке. Кстати, именно этим калькулятором я пользовался при расчете комплексных чисел ТОЭ, когда учился в университете. Пользоваться им крайне просто. Для перевода в разные формы используется установка нужного «флажка».

Если на руках имеется реальный калькулятор, который Вы купили в канцелярском магазине, и он обладает возможностью расчета комплексных чисел, то внимаем. Сейчас расскажу как им пользоваться.

1. Чтоб перевести комплексное число 5+3i из алгебраической формы в показательную, нажимаем клавиши в следующей последовательности:

Источник

Как преобразовать комплексное число из алгебраической формы в экспоненциальную форму и наоборот. Приведите пример

С алгебраической формой комплексного числа мы уже познакомились, 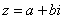– это и есть алгебраическая форма комплексного числа.

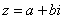
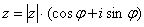
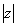
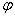
Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:
, где – это модуль комплексного числа, а – аргумент комплексного числа. Не разбегаемся, всё проще, чем кажется.

Изобразим на комплексной плоскости число 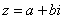. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что

Модулем комплексного числа 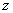называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.

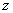
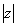
Модуль комплексного числа стандартно обозначают: или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 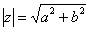. Данная формула справедлива для любых значений «а» и «бэ».

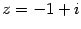
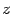
Пример 17.7 Пусть . Напишите показательную форму числа .

Решение. Находим модуль и аргумент числа:

Следовательно, показательная форма комплексного числа такова:

Пример 17.8 Комплексное число записано в показательной форме

Найдите его алгебраическую форму.

Решение. По формуле Эйлера

Итак, алгебраическая форма числа: .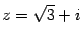

Распечатайте эти вопросы и запишите присланный регистрационный номер в левый верхний угол титульного листа.

Защищать работу можно у любого преподавателя кафедры «Высшая математика».

Расписание консультаций расположено в 7 корпусе рядом с аудиторией 7-310.

Источник

Калькулятор комплексных чисел. Вычисление выражений с комплексными числами

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Калькулятор комплексных чисел

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

Комплексные числа

Комплексные числа — это числа вида x+iy , где x , y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i 2 = -1 ).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi 2 = (ac — bd) + (bc + ad)i
• деление:

Примеры

Найти сумму чисел 5+7i и 5.5-2i :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: 5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: 12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: 2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: 75-50i / (3+4i) = 1 — 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a 2 + b 2 )
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: e z = e a ·cos(b) + i·e a ·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4 2 + (-3) 2 ) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy , где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ) , где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·e iφ , где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

• Найдём радиус (модуль) комплексного числа r: r = √(1 2 + 1 2 ) = √2
• Найдём аргумент числа: φ = arctan(

Источник