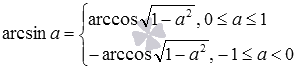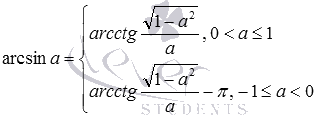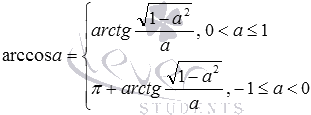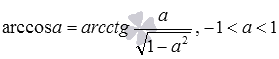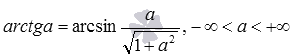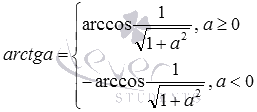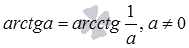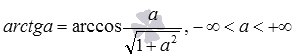Арксинус и арккосинус. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Арксинус и арккосинус − теория, примеры и решения
Функция арксинус и ее график
Как известно, функция синус определена в интервале [−∞;+∞] и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
 |
Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:
 , , , , , ,  и т.д. и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
Функция (1) − это функция, обратная к функции
График функции арксинус можно получить из графика функции 
 |
Свойства функции арксинус.
- Область определения функции:
.
- Область значений функции:
.
- Функция является нечетной:
.
- Функция возрастает.
- Функция непрерывна.
Решим тригонометрическое уравнение
При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке 
 |
В отрезке 
 |
Таким образом уравнение (3) имеет два решения в отрезке 
 |
 |
которые совпадают при |a|=1.
Поскольку функция синус периодичная с основным периодом 2π, имеем
 |
Тогда получим решение (2) в виде
Решения (3) и (4) удобно представить одним уравнением:
Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).
При a=1, arcsin a и π−arcsin a совпадают (т.к. 
При |a|=−1, из (3) и (4) следует:
Но поворот 

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:
Пример 1. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (5):
Пример 2. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (5):
Функция арккосинус и ее график
Как известно, функция косинус определена в интервале [−∞;+∞] и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.
 |
Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:
 , , , , , ,  и т.д. и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
Функция (8) − это функция, обратная к функции
График функции арксинус можно получить из графика функции 
 |
Свойства функции арксинус.
- Область определения функции:
.
- Область значений функции:
.
- Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
- Функция убывает.
- Функция непрерывна.
Решим тригонометрическое уравнение
При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t1=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t2=−arccos a(см. Рис.6):
 |
Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.
Поскольку функция косинус периодичная с основным периодом 2π:
 |
то общее решение (9) имеет следующий вид:
При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:
Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:
 |
Пример 1. Решить тригонометрическое уравнение:
Решение. Воcпользуемся формулой (10):
Так как 
Пример 2. Решить следующее тригонометрическое уравнение:
Решение. Используя формулу (10), имеем
Так как 

Пример 3. Решить следующее тригонометрическое уравнение:
Решение. Используя формулу (10), имеем
С помощью онлайн калькулятора вычисляем : 
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.
В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.
Навигация по странице.
Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.
Синус арксинуса, косинус арккосинуса и т.п.
Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Арксинус синуса, арккосинус косинуса и т.п.
Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.
Связи между arcsin, arccos, arctg и arcctg противоположных чисел
Формулы этого блока показывают, как арксинус, арккосинус, арктангенс и арккотангенс отрицательного числа выражаются через arcsin , arccos , arctg и arcctg противоположного ему положительного числа. Эти формулы позволяют избавиться от работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами отрицательных чисел, и перейти к работе с этими аркфункциями от положительных чисел.
Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.
Синус от арккосинуса, тангенс от арксинуса и иже с ними
На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.
Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид 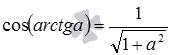
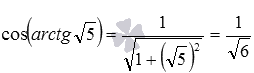
Другой пример: используя формулу синуса арккосинуса вида 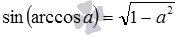
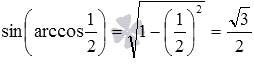
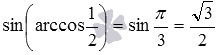
Осталось показать вывод записанных формул.
Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.
Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств 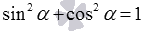
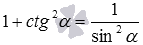
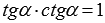
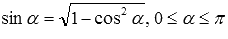
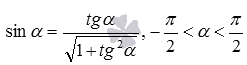
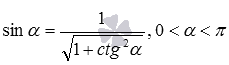
Вот краткая запись вышеперечисленных выкладок:
- так как
, то
;
- так как
, то
;
- так как
, то
.
По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:
- так как
, то
;
- так как
, то
;
- так как
, то
.
Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:
- так как
, то
при
;
- так как
, то
при
;
- так как
, то
при
.
Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как 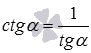
arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.
По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:
Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:
Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:
Наконец, вот ряд формул с арккотангенсом:
Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.
Для примера, докажем, что 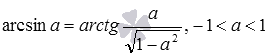
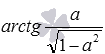
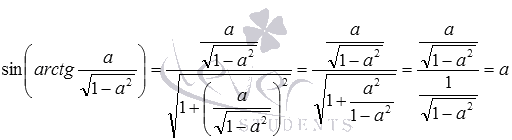
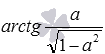
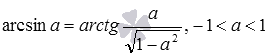
По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.
В заключение этого пункта покажем пример использования полученных формул. Для примера вычислим с их помощью, чему равен синус арккотангенса минус корня из трех. Обратившись к формуле вида 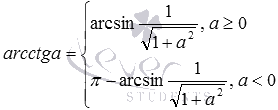
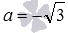
В данном примере мы могли вычислить требуемое значение и непосредственно: 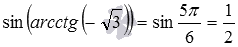
Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида 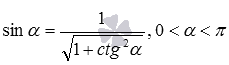
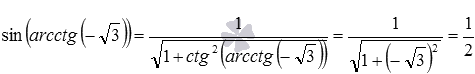
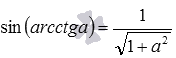
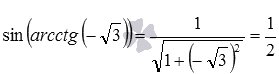
Некоторые другие формулы
Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin , arccos , arctg и arcctg , еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.
Для примера возьмем формулу половинного угла 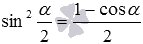
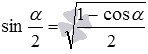

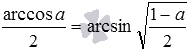
Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin , arccos , arctg и arcctg .
В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin , arccos , arctg и arcctg , сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

 .
. .
. .
.
 .
.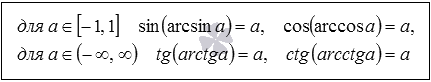

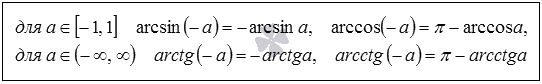
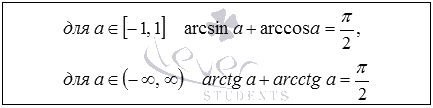

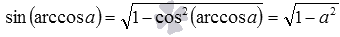 ;
;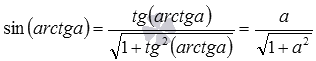 ;
;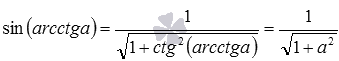 .
.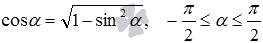 , то
, то 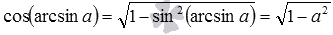 ;
;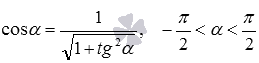 , то
, то 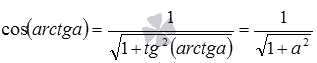 ;
;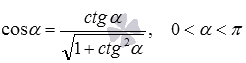 , то
, то 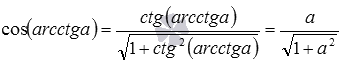 .
.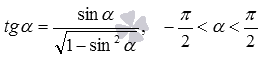 , то
, то 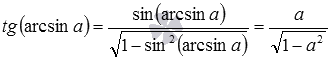 при
при 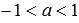 ;
;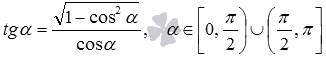 , то
, то 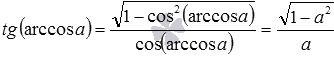 при
при 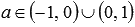 ;
;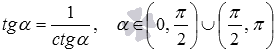 , то
, то 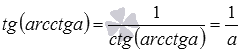 при
при 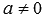 .
.