Перевод линейной скорости в угловую калькулятор

Линейная скорость через угловую

Мгновенной (истинной) скоростью ($\overline$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):

$\Delta \overline$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $\Delta t$.

Выражение линейной скорости через угловую скорость

Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.

Так как вектор перемещения $\Delta \overline$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $\Delta \overline$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.

Скорость прохождения пути ($s$) определяют:

Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.

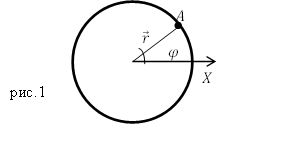
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($\varphi $), который образует радиус-вектор ($\overline$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).

Быстроту изменения угла поворота $\varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $\omega $. Угловая скорость равна:

Вращение называют равномерным, если угловая скорость постоянна $\omega =const$. При равномерном вращении $\omega $ можно называть угловой частотой.

Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$\ R=const$, то длину дуги найдем как:

Продифференцируем обе части выражения (4) по времени, имеем:

Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:

Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ — радиус кривизны траектории в месте нахождения частицы.

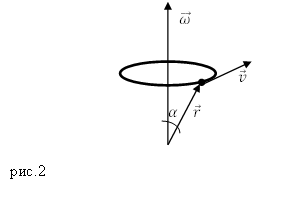
В векторном виде выражение (6) записывают так:

$\overline$ — вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:

где $\alpha $ — угол между вектором угловой скорости и $\overline.$

Угловая скорость через линейную

Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:

Или используя формулу (8) угловую скорость выразим как:

Примеры задач с решением

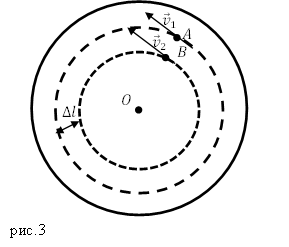
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $\Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($\omega $)?

Решение. Основой для решения задачи будет формула:

Угловые скорости движения точки A и B одинаковы ($<\omega >_A=<\omega >_B$), запишем выражение для каждой из этих скоростей используя (1.1):

$R_1$ — расстояние от точки O до точки A; $R_2=R_1-\Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:

Найдем угловую скорость точки A:

Ответ. Угловая скорость всех точек диска равна $\omega =\frac<\Delta l>$

Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с законом: $\varphi \left(t\right)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени, равный $t’=1\ (с)$.

Решение. В качестве основы для решения задачи воспользуемся формулой:

Используя уравнение $\varphi \left(t\right)$ и связь угла поворота и угловой скорости найдем $\omega $:

Подставим результат (2.2) в (2.1), имеем:

Вычислим искомую скорость:

\[v=1\cdot 3\cdot 5\cdot 1^2=15\ \left(\frac<м><с>\right).\]

Ответ. $v\left(t’\right)=15\frac<м><с>$

Источник

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник

Перевод угловой скорости в линейную формула

‘);> //—>
Угловая скорость — это физическая величина, характеризующая скорость вращения точки вокруг центра вращения.

Линейная скорость — это физичекая величина, характеризующая скорость, с которой точка движется по окружности вокруг центра вращения.

Формула перевода угловой скорости в линейную:

V — линейная скорость;
R — радиус окружности;
n — угловая скорость.

для справки D = 2 * R — диаметр окружности.

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

Для сложных расчетов по переводу нескольких единиц измерения в требуемую (например для математического, физического или сметного анализа группы позиций) вы можете воспользоваться универсальными конвертерами единиц измерения.

На этой странице представлен самый простой онлайн переводчик единиц измерения м/с в об/мин. С помощью этого калькулятора вы в один клик сможете перевести об/мин в м/с (обороты в минуту в метры в секунду) и обратно

Переход от угловой к линейной скорости.

Сегодня смотрел на детей, катающихся на карусели, и подумал — а интересно, с какой скоростью они крутятся.
Подумав еще, понял, что ответить на этот вопрос очень просто, достаточно подсчитать, сколько оборотов в минуту они совершают.

Зная число оборотов в минуту, можно найти угловую скорость в радианах в секунду — за один оборот угол меняется на радиан, за минуту — радиан, и соответственно за секунду — радиан.

Это угловая скорость — радиан/сек. Переход к линейной тривиален — углу в 1 радиан соответствует дуга окружности равная радиусу, соответственно,

Вот и все, а ниже калькулятор. Скорость в м/с приводит к км/час, чтобы было понятнее.

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Источник