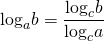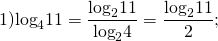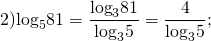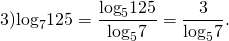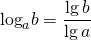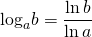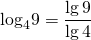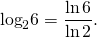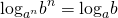Перевод логарифма к другому основанию - Uchenik.top

Содержание

Свойства логарифмов. Шпаргалка с формулами.

Любую значимую логарифмическую задачу невозможно решить, не зная особых правил логарифмов. А точнее – основных свойств. К счастью, этих свойств совсем не много и выучить их не составит труда. Но знать их нужно как слева направо, так и в обратную сторону.

Рассмотрим отдельные свойства более детально:

Логарифмический ноль. Элементарное свойство, которое нужно обязательно помнить. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Логарифмическая единица. Еще одно простое свойство: если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.

Основное логарифмическое тождество. Отличное свойство, превращающее четырехэтажное выражение в простейшую b. Суть этой формулы: основание a, возведенное в степень логарифма с основанием а, будет равно b.

Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2х логарифмов, у которых будут одинаковые основания. И так невычислимые логарифмы становятся простыми.

Логарифм частного. Здесь ситуация схожая с суммой логарифмов. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.

Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽ . Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф

Вынесение показателя степени из логарифма. Тут действуют целых 3 правила. Все просто: если степень находится в основании или аргументе логарифма, то ее можно вынести за пределы логарифма, в соответствии с этими формулами:

Формулы перехода к новому основанию. Они нужны для выражений с логарифмами, у которых разные основания. Такие формулы в основном используются при решении логарифмических неравенств и уравнений.

Второе свойство применяется, когда меняется местами аргумент и основание логарифма, при этом логарифм переносится в знаменатель.

Напоминаем про сервис грант-на-вуз.рф . Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф !

Мы разобрали основные свойства логарифмов. Теперь ни одно неравенство или уравнение не останется нерешенным 😉

Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:

Источник

Переход к новому основанию логарифма

Когда требуется осуществить переход к новому основанию логарифма, пользуются одним из свойств логарифмов —

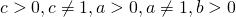
0,c \ne 1,a > 0,a \ne 1,b > 0\]» title=»Rendered by QuickLaTeX.com»/>

(Для запоминания этой формулы удобно воспользоваться следующей ассоциацией: то, что вверху, идёт вверх, то, что внизу — идёт вниз.

b, стоящее вверху, под знаком логарифма, записываем снова вверху, в числителе, под знак логарифма с новым основанием.

a, стоящее внизу, в основании логарифма, записываем вниз, в знаменателе, под знак логарифма с новым основанием).

Примеры перехода к новому основанию логарифма:

Перейти можно к любому новому основанию (положительному и отличному от единицы).

В том числе, любой логарифм можно представить в виде частного десятичных логарифмов:

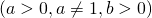
0,a \ne 1,b > 0)\]» title=»Rendered by QuickLaTeX.com»/>

Частный случай этой формулы —

— позволяет изменить основание логарифма на число, стоящее под знаком логарифма.

— дает возможность изменить основание логарифма в случае, когда оно может быть представлено в виде степени.

Источник

Логарифм. Свойства логарифмов

Рассмотрим равенство . Пусть нам известны значения и и мы хотим найти значение .

То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

Пусть переменная может принимать любое действительное значение, тогда на переменные и накладываются такие ограничения: o» title=»a>o»/> , 1″ title=»a<>1″/>, 0″ title=»b>0″/>

Если нам известны значения и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое действие, которое называется логарифмирование.

Чтобы найти значение , мы берем логарифм числа по основанию :

Логарифмом числа по основанию называется показатель степени, в которую надо возвести , чтобы получить .

То есть основное логарифмическое тождество:

o» title=»a>o»/> , 1″ title=»a<>1″/>, 0″ title=»b>0″/>

является по сути математической записью определения логарифма.

Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

Перечислим основные свойства логарифмов:

(o» title=»a>o»/> , 1″ title=»a<>1″/>, 0″ title=»b>0″/>, 0,

d>0″/>, 1″ title=»d<>1″/>

Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:

Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию:

10.

11.

12. (следствие из свойства 11)

Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

13.