Концентрация компонентов
Концентрацию компонент обычно откладывают в атомных процентах. В практическом материаловедении для удобства часто пользуются процентами по массе, но при анализе природы образующихся фаз, изучении закономерностей, определяющих предельные концентрации твердых растворов, и в других подобных случаях следует пользоваться атомными процентами.
Для систем, в которых одним из компонентов является полупроводник (химический элемент или соединение), наряду с диаграммами, построенными в обычном масштабе, строят диаграммы, на которых в области, примыкающей к полупроводнику, концентрацию легирующего компонента в атомных процентах наносят в логарифмическом масштабе (рис.5.3в), либо строят отдельно часть диаграммы, примыкающую к полупроводниковому компоненту, откладывая концентрацию второго компонента в атомах на кубический сантиметр тоже в логарифмическом масштабе (рис.5.3а).
Это вызвано тем, что концентрацию носителей заряда в полупроводниках измеряют в электронах (или дырках) на кубический сантиметр, и в тех случаях, когда легирующие добавки являются поставщиками носителей заряда, удобно концентрацию носителей и примесей измерять в одних единицах.
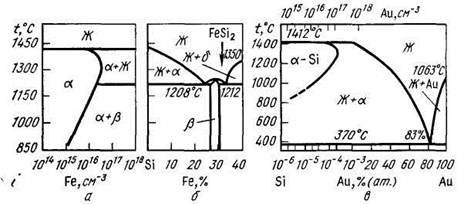 |
| Рис. 5.3. Т–Х -ДФР двухкомпонентных систем с ограниченной растворимостью компонент: а — концентрация в атомах на кубический сантиметр; б — в атомных процентах в линейном масштабе; в — в атомных процентах; в области, примыкающей к полупроводнику, атомные проценты легирующего компонента отложены в логарифмическом масштабе. |
Кроме того, предельная растворимость примесей в полупроводниках, как правило, очень мала
(0,1– 0,01) % ат. и реально используемое легирование по концентрации составляет (10 14 –10 19 ) ат/см 3 , т.е. (10 6 –10 –1 ) % ат. В этих условиях важно показать на диаграммах фазовые области, в которых концентрация компонентов в области малых концентраций изменяется на порядок величины. Логарифмический масштаб позволяет это сделать, тогда, как в обычном масштабе область концентраций меньше 0,1 % сливается с осью ординат.
Пересчет концентраций компонентов из одного масштаба в другой (ат.% в % по массе) осуществляют по следующим формулам:
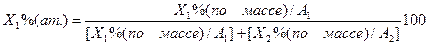 | (5.5) |
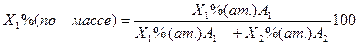 | (5.6) |
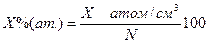 | (5.7) |
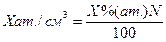 | (5.8) |
Хат/см 3 – (обычно пишут Хсм -3) количество атомов примеси в 1 см 3
N- общее число атомов в 1 см 3
N=
V – объем элементарной ячейки
Задача 5.2. Подсчитать количество атомов, приходящихся на долю одной элементарной ячейки в решетках Браве.
Дата добавления: 2014-01-11 ; Просмотров: 1203 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Плавящимися промежуточными фазами
Промежуточные фазы, при плавлении которых составы твердой и жидкой фаз совпадают, называют конгруэнтно плавящимися фазами (рисунок 3.6.1). Если в качестве промежуточной фазы выступает химическое соединение АmВn (постоянного состава) и граничные растворы на основе компонентов А и В имеют узкие области гомогенности и ими можно пренебречь, то диаграмма состояния описывает фазовые равновесия между практически чистыми компонентами А, В и химическим соединением АmВn (рисунок 3.6.1, а). На диаграмме химическому соединению соответствует ордината, проведенная из точки на координатной оси, отвечающей его составу AmBn. Химическое соединение АmВn кристаллизуется (или плавится) при постоянной температуре tm1 , отвечающей точке максимума на ликвидусе. Такая точка называется сингулярной (точка m1). Именно она соответствует температуре плавления химического соединения.
Ордината делит диаграмму состояния на две части, каждая из которых может представлять собой диаграмму любого типа. В рассматриваемом случае (рисунок 3.6.1) получаются две диаграммы эвтектического типа.
Такие диаграммы состояния характерны для систем, образованных металлами и элементами, которые обладают и металлическими, и неметаллическими свойствами, а промежуточная фаза представляет собой химическое соединение с нормальной валентностью или полупроводниковую фазу. На рисунке 3.6.1, б представлена диаграмма с конгруэнтно плавящейся промежуточной фазой, которая в отличие от предыдущей характеризуется наличием области гомогенности, как в областях приграничных твердых растворов на основе обоих компонентов, так и на основе промежуточной фазы.
Кристаллизация рассматриваемого сплава в системе с устойчивой промежуточной фазой (рисунок 3.6.1) будет происходить аналогично кристаллизации сплавов в обычной эвтектической системе. При охлаждении сплава из жидкого состояния ниже линии ликвидус начинают выделяться кристаллы химического соединения AmBn. Состав жидкой фазы изменяется при кристаллизации по линии СE1. По мере понижения температуры в кристаллизационном интервале температур происходит увеличение количества выделяющихся кристаллов химического соединения (промежуточной фазы AmBn). Однако такая кристаллизация развивается лишь до температуры эвтектического превращения, и не завершается образованием ста процентов кристаллов этого соединения. Количество сохранившейся незакристаллизованной жидкости может быть определено по правилу рычага.
 |
| Рисунок 3.6.1 — Диаграмма состояния системы с конгруэнтно плавящимися промежуточными фазами. |
При достижении температуры эвтектической линии оставшаяся часть жидкости превращается в эвтектику (А+AmBn)э, представляющая собой физико-химическую смесь кристаллов компонента A и химического соединения AmBn. Окончательно структуру этого сплава можно представить в виде первичных кристаллов химического соединения и эвтектики (рисунок 3.6.2). Первичные кристаллы промежуточных фаз постоянного состава могут иметь игольчатую, пластинчатую, полиэдрическую, дендритную (разветвленную) форму.
 | Рисунок 3.6.2 — Диаграмма фазового равновесия системы с устойчивым (конгруэнтно плавящимся) химическим соединением |
Если на диаграмме состояния с наличием химического соединения концентрацию элементов отложить в атомных процентах, то по диаграмме состояния (рисунок 3.6.3) можно определить химическую формулу соединения.
 | Рисунок 3.6.3. Определение формул двух химических соединений по диаграмме фазового равновесия Cu-Mg |
Пересчет массовых процентов в атомные производится по формуле:

Обратный пересчет атомных процентов в массовые производится по формуле:
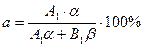
где; A1; B1 – атомные веса компонентов A и B; a, b атомные % компонента A и B; a, b – массовые % компонента A и B.
Например, в системе Cu-Mg при 16 % и 44 % (масс.) Mg пересчет в атомные (33,3 % и 66,7 %, соответственно) показывает, что для 33,3% (ат) на 1 грамм-атом Mg приходится 2 грамм-атома Cu, следовательно, его формула Cu2Mg, а для 66,7% (ат) Mg, на 1 грамм-атом меди приходится 2 грамм-атома Mg. Следовательно формула химического соединения CuMg2.
Для диаграмм состояния с конгруэнтно плавящимися промежуточными фазами переменного состава (g-фаза на рисунке 3.6.1, б) характерны сравнительно широкие области граничных a- и b-растворов, и значительная растворимость компонентов А и В в химическом соединении АmВn, на основе которого образуется g-твердый раствор. Линия m1AmBn в области промежуточной g-фазы показывает средний стехиометрический состав соединения AmBn. Область m1bb1AmBn левее линии представляет собой g-твердый раствор компонента А в АmBn, а область правее линии m1cc1AmBn — g-твердый раствор компонента B в АmBn . В случае образовании твердых растворов замещения атомы компонента А замещают в подрешетке соединения АmBn атомы компонента В, и наоборот. Таким образом в пределах g-области твердые растворы на основе химического соединения АmВn содержат избыток одного из компонентов относительно стехиометрического состава или оба компонента, соответствующих стехиометрическому составу соединения АmВn.
Все твердые растворы в области гомогенности промежуточной g-фазы являются ненасыщенными. Насыщенными относительно кристаллов граничных a или b-растворов при охлаждении становятся только те g-растворы, фигуративные точки которых, попадая на кривые сольвуса bb1 и сс1 оказываются затем в двухфазных областях a+g и b+g. Тогда из кристаллов промежуточной g-фазы при охлаждении в связи с переменной ограниченной растворимостью в твердом состоянии выделяются вторичные a или b-кристаллы, которые в равновесных условиях, чаще всего, располагаются в виде пленок по границам зерен твердого раствора.
Определение атомных и весовых количеств элементов. Перевод атомных количеств в весовые проценты. Расчет средних содержаний
Лабораторная работа № 1
Задание:
Даны количественные содержания основных окислов по результатам силикатного анализа. Требуется пересчитать весовые проценты окислов SiO2, Al2O3, Fe2O3, FeO, TiO2, MnO, MgO, CaO, Na2O, K2O, P2O5, SO3 на весовые проценты элементов, с составлением таблицы используя нижеприведенный порядок расчетов. Найти дисперсию и стандартное отклонение по каждому элементу.
Ход работы:
1. Взять данные по атомному весу элементов О (16), Si(28), Al (27), Fe (55,85), Ti (48), Mn (55), Mg (24), Ca (40), Na (23), K (39), P (31).
2. Рассчитать молекулярный вес каждого окисла.
3. По соотношениям молекулярного веса окисла и его атомного веса, молекулярного веса окисла и его содержания в весовых процентах рассчитываем концентрацию элемента в весовых процентах, исходя из пропорции:
— cодержание элемента в вес.%– атомный вес элемента;
— cодержание окисла в вес.% – молек.вес окисла
Пример расчета для оксида кремния SiO2.
Атомный вес О=16; атомный вес Si=28; молекулярный вес SiO2=60;
К примеру, содержание SiO2 в вес.% =70.4%.
70,4% – 60, где Х содержание Si в SiO2 в вес.%.
В приведенном расчете множитель 28/60 представляет собой частное от деления атомного веса определяемого элемента, в данном случае Si, на молекулярный вес окисла SiO2. Этот множитель остается постоянным применительно к любому значению содержания SiO2 в весовых %. Данная схема определения весовых количеств элемента с использованием атомных количеств применима к расчету содержаний любого элемента в весовых процентах по процентному содержанию его окисла. Поэтому нет необходимости в каждом конкретном случае составлять вышеприведенную пропорцию и решать ее. Следует принять отношение атомного веса элемента к его молекулярному весу за своего рода константу, расчетный коэффициент К, для использования при определении процентного содержания элементов по содержанию их окислов в весовых процентах. Определяем расчетный коэффициент К для каждого элемента по формуле, включающей в числители атомный вес элемента А, в знаменателе- молекулярный вес окисла:
Вычислить расчётные коэффициенты:
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
| K |
4. Результаты пересчетов выносим в таблицу 5.
| № пробы | Содержание в вес. % | ||||||||
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
5. Вычисляем дисперсию и стандартное отклонение
Дисперсия и стандартное отклонение позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним. Для выборки Х1, Х2, … Хn выборочная дисперсия (обозначаемая символом S 2 задается следующей формулой:
В общем случае выборочная дисперсия — это сумма квадратов разностей между элементами выборки и выборочным средним, деленная на величину, равную объему выборки минус один:
где X̅ — арифметическое среднее, n — объем выборки, Xi — i-й элемент выборки X.
Наиболее практичной и широко распространенной оценкой разброса данных является стандартное выборочное отклонение. Этот показатель обозначается символом S и равен квадратному корню из выборочной дисперсии:
| № пробы | Содержание в вес. % | ||||||||
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
| 33,09 | |||||||||
| 29,78 | |||||||||
| 32,15 | |||||||||
| 28,41 | |||||||||
| 28,56 | |||||||||
 | 30,4 | ||||||||
| S 2 | 4,51 | ||||||||
| S | 2,12 |
Ни выборочная дисперсия, ни стандартное выборочное отклонение не могут быть отрицательными. Единственная ситуация, в которой показатели S 2 и S могут быть нулевыми, — если все элементы выборки равны между собой.
Дисперсия и стандартное отклонение позволяют оценить разброс данных вокруг среднего значения, иначе говоря, определить, сколько элементов выборки меньше среднего, а сколько — больше. Стандартное отклонение позволяет оценить величину колебаний элементов выборки вокруг среднего значения.





