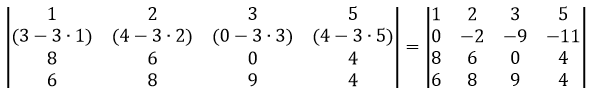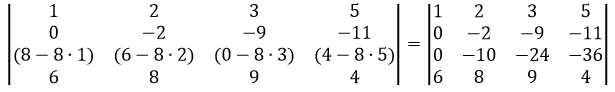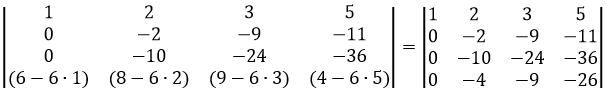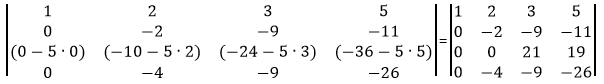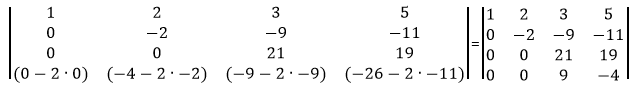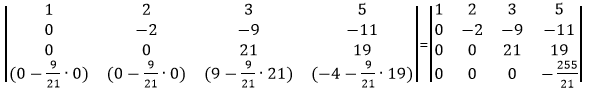Перевод матрицы к треугольному виду

Приведение определителя матрицы к треугольному виду

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.

Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.

Пример

Найдем определитель матрицы четвертого порядка.

Сделаем элемент a_2,1 равный нулю.

Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3

Сделаем элемент a_3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8

Сделаем элемент a_4,1 равный нулю.

Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6

Сделаем элемент a_3,2 равный нулю.

Из строки №3 вычитаем строку №2, умноженную на 5

Сделаем элемент a_4,2 равный нулю.

Из строки №4 вычитаем строку №2, умноженную на 2

Сделаем элемент a_4,3 равный нулю.

Из строки №4 вычтем строку №3, умноженную на 9/21.

Умножим элементы матрицы находящиеся на диагонали.

Источник

Калькулятор матриц — действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Как пользоваться калькулятором матриц

1. Выберите матрицу (или матрицы) с помощью переключателей ( )
2. Укажите размер с помощью выпадающих списков под матрицей ( × )
3. Заполните элементы (нулевые элементы можно не заполнять.)
4. Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
5. Нажмите кнопку .
6. Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам

Что умеет наш калькулятор матриц?

Вычисление выражений с матрицами

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + — * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: ^T
• Возведение в целую степень: ^

Примеры корректных выражений

• Cложение двух матриц: A+B , (A)+(B) , ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A — 0.5B)^5
• Произведение транспонированной матрицы на исходную: A^TA
• Обратная матрица в квадрате для B: B^-2

Что такое матрица?

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: A_n×m .

Примеры матриц

Элементы матрицы

Элементы A обозначаются a_ij , где i — номер строки, в которой находится элемент, j — номер столбца.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: a T _ij = a_ji

Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — a_ii

Единичная матрица E_n×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: A n

Обратная матрица A −1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A -1 ×A = A×A -1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij+b_ij

Разность матриц A_n×m и B_n×m — матрица C_n×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: с_ij=a_ij-b_ij

Умножение матриц A_n×k и B_k×m — матрица C_n×m, у которой элемент (c_ij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: c_ij = a_i1·b_1j + a_i2·b_2j + . + a_ik·b_kj

Источник

Приведение матрицы к ступенчатому виду

Матрица — математический объект, представленный в форме квадратной или прямоугольной таблицы, содержащей определенное число строк и столбцов, именуемых порядками. Матрицы могут различаться размерами и содержанием. Матрицы позволяют упорядочить записи систем линейных уравнений, что ведет к удобному поиску их результатов. Работа с матрицами предполагает приведение их к стандартному виду.
В математике множество разнообразных видов матриц. Все элементы нулевой матрицы равны нулю, а число строк и столбцов может быть совершенно разным.
Матрица квадратного типа имеет одинаковое количество строк и столбцов. Матрица простейшего вида вектор-столбец имеет три численных значений, расположенных в столбец. Вектор-строка содержит три численных элементов, размещенных в одну строку. В диагональной матрице числовые значения имеют лишь элементы главной диагонали, остальные равны нулю. Начинается диагональ с элемента в правом верхнем углу и заканчивается в последнем столбце последней строки. Диагональный тип может иметь лишь квадратная матрица. Подвид диагональной матрицы — единичная, все числовые значения которой равны единицам. В канонической матрице не все компоненты основной диагонали равны единице, число строк и столбцов может быть разное, но, как и в единичной матрице, элементы, расположенные не на основной диагонали, равны нулю. Матрица треугольного типа является квадратной. Матрица, элементы которой, расположенные ниже главной диагонали, равны нулю, называется нижнетреугольной. В верхнетреугольной матрице числовые значения имеют элементы, расположенные на основной диагонали и под ней. Над диагональю элементы имеют нулевое значение.

Матрица, имеющая «ступени» из нулей, называется ступенчатой. В данном типе матриц диагональ из нулей не обязательно должна быть основной. Элементы под диагональю, как и на диагонали, должны иметь нулевые значения. Элемент в углу каждой ступеньки — ненулевой. Первый ненулевой элемент строки обязательно располагается правее первого ненулевого элемента строки предыдущей. Все элементы под 1-м ненулевым элементом строки имеют нулевые значения. Если ступенчатая матрица имеет нулевую строку, строки ниже нее тоже не имеют числовых значений. Т.е нулевые строки — последние. Для приведения матрицы к ступенчатому виду следует определить ее детерминант. Задание выполнимо, если детерминант больше или меньше нуля, в противном случае (равен нулю) привести матрицу к ступенчатому виду нельзя.

Любую матрицу несложно привести к ступенчатой форме, используя следующие элементарные преобразования:
— перестановка двух строк (столбцов);
— умножение строки (столбца) на любое, кроме нуля, число;
— сложение строки (столбца) с другой (другим), умноженной (умноженным) на любое, произвольно взятое (кроме нуля) число.

Приводим матрицу к ступенчатому виду:
1. Выбираем элемент, отличный от нуля в 1-м столбце. Если выбранный элемент (ведущий) расположен не в 1-й строке, переставляем строку с ведущим элементом на первую (ведущую) строку. Если элементы 1-го столбца равны нулю, исключаем его и переходим к следующему.
2. Делим элементы ведущей строки на ведущий элемент. Преобразования закончены при условии, что ведущая строка последняя.
3. К строке, расположенной под ведущей, добавляем ведущую, предварительно умноженную на число, чтобы элементы стоящей ниже строки стали равняться нулю.
4. Исключаем строку и столбец с ведущим элементом на пересечении.
Повторяем те же действия с оставшейся частью матрицы.

Привести матрицу к ступенчатому виду вам поможет онлайн калькулятор. Выберите размерность и введите значение ее элементов.

Источник