Перевод напряженности поля в плотность потока энергии

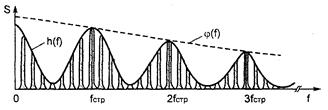
Плотность потока мощности и эквивалентная изотропная излучаемая мощность

Чтобы наземные устройства могли принимать сигналы со спут­ника, необходимо создать у поверхности Земли определенную на­пряженность электромагнитного поля (или плотность потока мощ­ности электромагнитных волн). Мощность электромагнитных волн, излучаемых антенной, является важнейшей характеристикой пере­дающей системы. Излучать их равномерно во все стороны, то есть изотропно, при спутниковом телевизионном вещании нецелесооб­разно и в большинстве случаев недопустимо. Поэтому излучаемая энергия электромагнитных волн концентрируется антенной в узкий луч и направляется на выбранную земную поверхность.

(2.2)

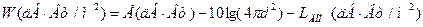
Более точно расстояние можно определить по формуле:

, (2.3)

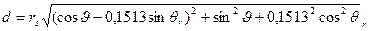
Для определения значения плотности потока мощности по из­вестной величине эквивалентно изотропной излучаемой мощности (без учета потерь) можно руководствоваться упрощенной формулой (2.4) или графической зависимостью, представленной на рис. 2.3

Плотность потока мощности является очень важной характери­стикой для приема со спутников-ретрансляторов. Она позволяет оценить возможность уверенного приема в данной географической точке на антенну соответствующего размера и при выбранных зна­чениях коэффициента шума и усиления малошумящего усилителя-конвертера. Величина плотности потока мощности влияет на сис­тему спутникового телевизионного вещания. Увеличение ее приво­дит к упрощению и удешевлению наземных приемных устройств, однако усложняет и повышает стоимость передающих систем спут­ника. Уменьшение ППМ, наоборот, удорожает наземные приемные устройства при одновременном удешевлении спутника. Необходи­мая ППМ у поверхности Земли определена путем экономических расчетов с оптимизацией стоимости как приемных наземных уст­ройств, так и передающих спутниковых систем и выбрана с учетом электромагнитной совместимости с наземными службами, т.е. с учетом минимальных взаимных помех

Е, дБ Вт

Рис. 2.3. Графическая зависимость ЭИИМ (Е) от плотности потока мощно­сти (W), позволяющая оперативно взаимно пересчитывать эти величины

Форма зоны покрытия зависит от точки пересечения (точки при­целивания) основного лепестка излучения антенны спутника с зем­ной поверхностью. Например, точка прицеливания российского спутника ГАЛС-1 находится между Москвой и Саратовом и форма зоны покрытия представляет собой вытянутый эллипс.

Границы зоны покрытия очерчены контурами на географической карте с определенными уровнями ППМ или ЭИИМ. Размеры ее стремятся сделать минимальными, чтобы снизить необходимую мощность передатчика спутника с целью его удешевления.

Некоторые предельные мешающие значения ППМ от спутников-ретрансляторов для радиорелейных, сотовых, спутниковых теле­фонных систем и т.д. в зависимости от угла е(угла между направ­лением прихода мешающей электромагнитной волны и горизон­тальной горизонтальной плоскостью) приведены в табл.2.1

Предельная плотность потока мощности (W) для угла ,

Как видно, плотности потока мощности ограничиваются в диапа­зонах частот выделенных для спутников ФСС.

Требования к равномерности спектра передаваемого теле­визионного сигнала.Для снижения вероятных помех другим сис­темам связи и приемным устройствам всегда необходимо, чтобы спектральная плотность передаваемого сигнала была бы равно­мерной в занимаемой полосе частот, чтобы выбросы энергии не превышали предельно допустимое значение. Известно, что частот­но-модулированный телевизионный сигнал имеет неравномерный энергетический спектр, зависящий от передаваемых сюжетов изо­бражения. Энергия в его спектре распределяется не непрерывно, а в виде дискретных энергетических зон (выбросов,), которые распо­лагаются вокруг частот строчной и кадровой разверток (рис. 2.4).

Рис. 2.5. Временная зависимость амплитуды сигнала для дисперсии аналогового сигнала в системе D-MAC/packet

Для исключения заметности на экране сигнала дисперсии, про­являющегося в виде мерцающих светлых точек, в приемных уст­ройствах применяют хорошо известные схемы построчной фикса­ции (схемы привязки) уровня, которые устанавливают по всему по­лю кадра равномерный уровень черного и тем самым практически подавляют сигнал дисперсии.

Рис. 2.6. Распределение плотности потока мощности спутника TDF-1

Шумы

□ из внешних принятых шумов ( атмосферные шумы, галакти­ческие шумы, шумы Солнца, Земли и др.)

□ из внутренних шумов приемного устройства (эквивалентные
шумы антенны, шумы коаксиальной линии питания, шумы предва­рительного усилителя, смесителя и т.д.). Они вызывают ухудшение

приема, снижают чувствительность приемного устройства, так как ограничивают прием минимального полезного сигнала по уровню.

Источник

Энергия и мощность электромагнитного поля

Энергией называется общая количественная мера различных форм движения материи, а мощностью называется работа, производимая в единицу времени.

Электромагнитное поле обладает энергией, значит, ее можно определить. При этом векторы поля и электродинамические характеристики средысчитаем известными.

Баланс энергии электромагнит­ного поля

Вначале сформулируем уравнение баланса энергии в общем виде. Для этого рассмотрим объем V, заполненный однородной изо­тропной средой и ограни­ченный поверхностью S. Пусть в этом объеме за счет действия сторонних источни­ков выделяется электромаг­нитная энергия. Очевидно, что мощность, выделяемая сторонними источниками, может расходо­ваться на потери в среде, на изменение запаса энергии внутри объема и на излучение в окружающую среду через поверхность S.

При этом должно выполняться следующее равенство:

Уравнение (4.1) дает качественное представление об энергетических соотношениях в электромагнитном поле. Для определения количественных характеристик воспользуемся уравнениями Максвелла.

После скалярного умножения получим:

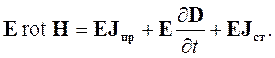(4.2)

Далее необходимо использовать формулу векторного анализа (1.26) и выразить из нее произведение Еrot Н, стоящие в правой части уравнения (4.2):

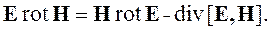(4.3)

Подставим это выражение в формулу (4.2) и перенесем произведение вектора напряженности электрического поля на вектор плотности сторонних токов в левую часть, а все остальные слагаемые – в правую. Кроме того, с помощью второго уравнения Максвелла заменим rot Е на производную по времени от вектора магнитной индукции с обратным знаком и с помощью формул (1.9), (1.14) выразим векторы индукции через соответствующие векторы напряженности поля и проницаемости.

Получим:

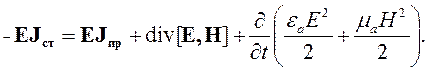(4.4)

Векторное произведение векторов Е и Н обозначается буквой П и называется вектор Пойнтинга:

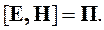(4.5)

Осталось проинтегрировать уравнение (4.4) по объему V. В результате получим:

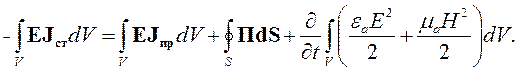(4.6)

В преобразовании уравнения (4.6) использована теорема Остроградского-Гаусса (1.33). Кроме того, в последнем слагаемом правой части уравнения изменен порядок операций интегри­рования и дифференцирования.

Левая часть уравнения (4.6) определяет мощность, отдаваемую сторонними токами в объеме V. Сторонний ток проводимости – это упорядоченное движение заряженных частиц. Для простоты положим, что векторы напряженности электрического поля и плотности сторонних токов коллинеарны. Если частицы тормозятся полем, ток отдает ему свою энергию. Для этого требуется, чтобы векторы напряженности электрического поля и плотности стороннего тока были направлены про­тивоположно. Значит, скалярное произведе­ние векторов Е и J_ст будет отрицательным и левая часть уравнения (4.5) станет положительной величиной. Такая ситуация характерна для работы некоторых передающих антенн.

Если векторы плотности стороннего тока и напряженности электрического поля направлены в одну сторону, заряженные частицы будут ускоряться полем, и ток станет отбирать у него энергию. Эту процедуру осуществляют разного рода приемные антенны, однако энергия, которую они могут отнять у поля в свободном пространстве, невелика.

Иначе обстоит дело в волноводах, которые служат для передачи энергии от источника к потребителю. На входном конце волновода сторонние силы реализуют процедуру возбуждения поля. Когда энергия достигает конца волновода, ее надо полностью отобрать у поля и передать потребителю. Для этого используются приемные устройства, преобразующие энергию электрической или магнитной составляющей поля в ток проводимости и передающие его дальше. В этом случае требуется отбирать у поля максимум энергии.

Реальная среда всегда обладает электропроводностью. Поэтому, зная напряженность электрического поля и электропроводность среды, можно найти мощность тепловых потерь, т. е. энергию, теряемую электромагнитным процессом за единицу времени.

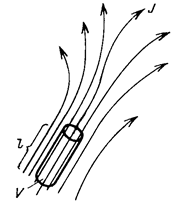Рис. 4.1. К определению мощности потерь

Обратимся к рис. 4.1, на котором изображена картина линий вектора плотности тока проводимости. В объеме протекания тока выделена цилиндрическая область V. Этот цилиндр имеет длину l и площадь основания S, а ось его совпадает с направлением вектора плотности тока проводимости. Для упрощения решения задачи область должна быть так мала, чтобы вектор плотности тока внутри нее можно было бы считать не зависящим от координат. В этом случае в соответствии с первым слагаемым правой части формулы (4.6) получим:

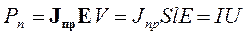(4.7)

Так как плотность тока проводимости и напряженность поля не зависят от координат, они вынесены из-под знака интеграла. Там остался только скалярный дифференциал объема. Его интегрирование по объему дает величину объема. В средней части формулы (4.7) объем цилиндра представлен как произведение площади его основания S на длину l, а параллельные векторы плотности тока и напряженности поля заменены их модулями. Ток I в последней части формулы определен как произведение площади основания цилиндра на плотность тока, а напряжение U – как произведение длины цилиндра на напряженность электрического поля.

Для выяснения физического смысла последнего слагаемого в правой части уравнения (4.6) рассмотрим частный случай. Предположим, что объем V окружен идеальной проводящей оболочкой, совпадающей с поверхностью S. Такая оболочка блокирует обмен энергией с внешней средой, и объем становится энергетически изолированным. В этом случае тангенциальная (касательная) составляющая напря­женности электрического поля на поверхности S будет равна нулю. Векторный дифференциал поверхности dS совпадает по направлению с ортом внешней нормали n₀. Следовательно, поверхностный интеграл в уравнении (4.6) будет равен нулю из-за того, что нормальная компонента вектор­ного произведения [Е, Н] определяется тангенциальными составляю­щими входящих в него векторов.

Предположим, кроме того, что электропроводность среды в объеме V равна нулю. Значит, тепловые потери исчезнут, и первый интеграл в правой части уравнения (4.6) также будет ра­вен нулю.

Получим:

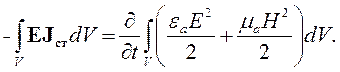(4.8)

В таком изолированном объеме без потерь мощность сторонних источников может расходоваться только на изменение запаса энергии электромагнитного поля. Значит, правая часть уравнения (4.8) равна скорости изменения энергии электро­магнитного поля, запасенной в объеме V, а интеграл в правой части этого уравнения равен энергии электромагнитного поля в объеме V:

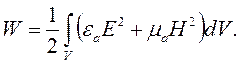(4.9)

Осталось выяснить физическую сущность поверхностного инте­грала в уравнении (4.6). Предположим, что потери внутри объема V отсут­ствуют и, кроме того, величина электромагнитной энергии остаетсяпостоянной.

B этом случае уравнение (4.6) примет следующий вид:

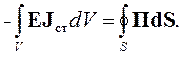(4.10)

Потерь в объеме нет, и запас энергии не меняется, значит, вся мощность сторонних источников должна излучаться в окружающее пространство. Следовательно, поток вектора Пойнтинга П через поверхность S равен излучаемой мощности, которую в уравнении (4.1) мы обозначили Р_Σ.

Таким образом, качественное уравнение (4.1) преобразовано в уравнение (4.6) с помощью которого можно проводить количественные оценки составляющих баланса мощности.

Рассмотрим частный случай отбора энергии электромагнитного поля сторонними источниками. Пусть энергия поступает в объем V из окружающего пространства. Часть ее преобразуется в тепло, а другая отбирается сто­ронними источниками. При этом количество электромагнитной энер­гии, запасенной в объеме V, не изменяется.

Урав­нение (4.6) в этом случае надо переписать в следующем виде:

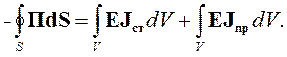(4.11)

Так как левая часть уравнения (4.11) представляет собой поток энергии, то вектор Пойнтинга является вектором плотности потока энергии. Направление вектора Пойнтинга в изотропной среде совпадает с направлением распространения энергии.

Плотность энергии электромаг­нитного поля

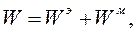(4.12)

где W э – энергия электрического поля, Вт*с:

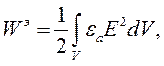(4.13)

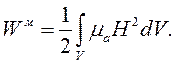(4.14)

Подынтегральные выражения в формулах (4.13) и (4.14) описывают объемные плотности энергии электрического и магнитного полей:

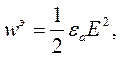	(4.15)
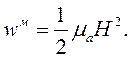	(4.16)

Сумма результатов вычислений по формулам (4.15) и (4.16) дает объемную плотность полной энергии электромагнитного поля.

Необходимо обратить внимание на следующий факт. Векторы напряженности электрического и магнитного полей удовлетворяют принципу суперпозиции. Это означает, что векторы напряженности полей, созданных разными источниками, складываются. Однако этот принцип не распространяется на энергию.

Для доказательства этого рассмотрим два поля, вектора напряженности которых равны Е₁, Н₁ и Е₂, Н₂ соответственно. Они существуют в одной области V и имеют энергии W₁ и W₂. Векторы напряженности суммарного поля определятся простым суммированием: Е = Е₁ + Е₂, Н = Н₁ + H₂. Энергию суммарного поля надо определять по формуле (4.9):

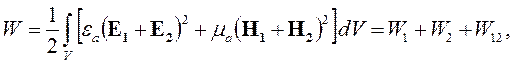(4.17)

где W₁₂ — взаимная энергия полей:

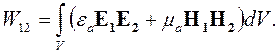(4.18)

Взаимная энергия может быть как положительной, так и отрицательной. Если же векторы Е₁ и Е₂, а также Н₁ и Н₂ взаимно перпенди­кулярны, то взаимная энергия полей равна нулю.

В переменном электромагнит­ном поле энергия непрерывно перераспределяется между электрическим и магнитным полем. Это перераспределение в каждой точке поля описывается уравнением (4.4). Однако его целесообразно переписать в ином виде:

Уравнение (4.19) является дифференциальной формой теоремы Пойнтинга.

Скорость распространения элек­тромагнитной энергии

Электромагнитная энергия распространяется в пространстве не мгновенно, а с некоторой скоростью. Для определения этой скорости в пространстве, в котором распространяется энергия, выделим энергетическую трубку (рис. 4.2). Форма трубки должна быть такой, что­бы ее боковая поверхность совпадала с направлением вектора Пойнтинга. То есть на боковой поверхности трубки нормальная составляющая векто­ра Пойнтинга должна быть равна нулю.

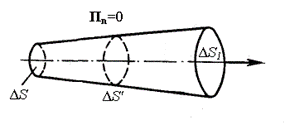Рис. 4.2. Энергетическая трубка

За время Δt через поперечное сечение труб­ки ΔS проходит энергия ΔW. Она сосредоточена в объеме ΔV между сечениями трубки ΔS и ΔS₁. Расстояние между этими сечениями равно Δl. При этих условиях скорость распространения энергии можно описать формулой:

Энергию ΔW, распространяющуюся вдоль трубки, можно определить интегрированием плотности энергии по площади сечения трубки и умножением результата на ее длину:

Положение этого сечения не важно, так как через любое сечение трубки за время Δt проходит вся энергия ΔW. При достаточно малых промежутках времени Δt вектор Пойнтинга можно считать неизменным, поэтому, кроме равенства (4.21) должно выполняться еще одно:

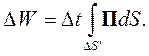(4.22)

Для того чтобы определить скорость переноса энергии надо разделить Δl на Δt и устремить Δt к нулю. Для этого надо формулу (4.22) разделить на формулу (4.21), выделить искомое отношение и выполнить предельный переход:

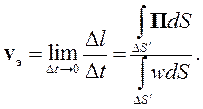(4.23)

Если векторы Е и Н постоянны в сечении ΔS, постоянными будут и вектор Пойнтинга П и объемная плотность энергии w.В этом случае соотношение (4.23) можно упростить, основываясь на том, что направ­ление вектора Пойнтинга совпадает с направлением распростра­нения энергии:

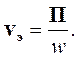(4.24)

Следовательно, скорость переноса энергии электромагнитным полем можно вычислить, разделив плотность потока энергии (вектор Пойнтинга) на плотность энергии.

Источник