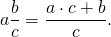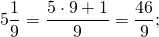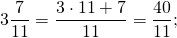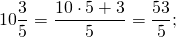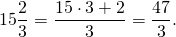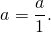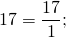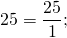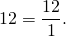Перевод неправильной дроби в смешанное число примеры - Uchenik.top

Содержание

Смешанные дроби или смешанные числа.

Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.

Как сделать из неправильной дроби правильную дробь?

Рассмотрим неправильную дробь \(\frac<21><9>\)

Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

После деления столбиком у нас появились неполное частное, его записываем в целую часть дроби. Остаток записываем в числитель, а делитель записываем в знаменатель.

Получаем дробь \(2\frac<3><9>\), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а \(\frac<3><9>\) – правильная дробь.

Смешанные дроби состоят из целой и дробной части.

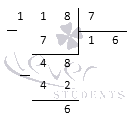
Рассмотрим еще одну неправильную дробь \(\frac<76><5>\)

Разделим ее столбиком:

Получили смешанную дробь \(15\frac<1><5>\)

Как смешанную дробь перевести в неправильную дробь?

Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:

Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.

Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.

Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.

Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.

Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.

Пример №1:
Представьте дробь в виде смешанного числа: \(\frac<508><17>\)

Решение:
Разделим дробь столбиком:

Ответ: Получили смешанную дробь \(29\frac<15><17>\)

Пример №2:
Представьте число в виде неправильной дроби: а) \(9\frac<2><3>\), б) \(1\frac<3><7>\)
Решение:
а) \(9\frac<2> <3>= \frac<9 \times 3 +2> <3>= \frac<29><3>\\\\\)
б) \(1\frac<3> <7>= \frac<1 \times 7 +3> <7>= \frac<10><7>\\\\\)

Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил \(\frac<2><5>\) от этого числа. Сколько задач решил Миша за первую неделю?

Решение:
У нас есть дробь \(\frac<2><5>\), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
\(120 \div 5 = 24\) задачи это одна часть или \(\frac<1><5>\)
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
\(24 \times 2 = 48\) задач
Ответ: за неделю Миша решил 48 задач.

Источник

Смешанные числа, перевод смешанного числа в неправильную дробь и обратно.

В этой статье мы поговорим про смешанные числа. Сначала дадим определение смешанных чисел и приведем примеры. Дальше остановимся на связи между смешанными числами и неправильными дробями. После этого покажем, как перевести смешанное число в неправильную дробь. Наконец, изучим обратный процесс, который называется выделением целой части из неправильной дроби.

Навигация по странице.

Смешанные числа, определение, примеры

Так мы подошли к определению смешанного числа.

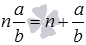
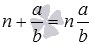
По определению смешанное число равно сумме свой целой и дробной части, то есть, справедливо равенство , которое можно записать и так: .

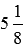
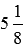
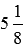
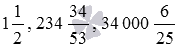
Приведем примеры смешанных чисел. Число — это смешанное число, натуральное число 5 – целая часть числа , а — дробная часть числа . Другими примерами смешанных чисел являются .

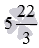
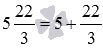
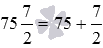
Иногда можно встретить числа в смешанной записи, но имеющие дробной частью неправильную дробь, например, или . Эти числа понимают как сумму их целой и дробной части, например, и . Но такие числа не подходят под определение смешанного числа, так как дробной частью смешанных чисел должна быть правильная дробь.

Число — это тоже не смешанное число, так как 0 не натуральное число.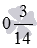

Связь между смешанными числами и неправильными дробями

Проследить связь между смешанными числами и неправильными дробями лучше всего на примерах.

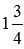
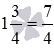
Пусть на подносе лежит торт и еще 3/4 такого же торта. То есть, по смыслу сложения на подносе находится 1+3/4 торта. Записав последнюю сумму в виде смешанного числа, констатируем, что на подносе находится торта. Теперь целый торт разрежем на 4 равные доли. В результате на подносе окажется 7/4 торта. Понятно, что «количество» торта при этом не изменилось, поэтому .

Из рассмотренного примера явно видна такая связь: любое смешанное число можно представить в виде неправильной дроби.

Из этого примера понятно, что неправильную дробь можно представить в виде смешанного числа. (В частном случае, когда числитель неправильной дроби делится нацело на знаменатель, неправильную дробь можно представить в виде натурального числа, например, 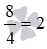, так как 8:4=2 ).

Перевод смешанного числа в неправильную дробь

Для выполнения различных действий со смешанными числами оказывается полезным навык представления смешанных чисел в виде неправильных дробей. В предыдущем пункте мы выяснили, что любое смешанное число можно перевести в неправильную дробь. Пришло время разобраться, как осуществляется такой перевод.

Рассмотрим пример перевода смешанного числа в неправильную дробь.

Представьте смешанное число 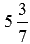в виде неправильной дроби.

Выполним все необходимые шаги алгоритма.

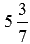
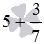
Смешанное число равно сумме его целой и дробной части: .

Чтобы закончить перевод исходного смешанного числа в неправильную дробь, осталось выполнить сложение дробей с разными знаменателями: .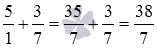

Краткая запись всего решения такова: .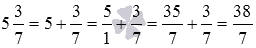

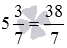
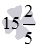
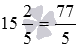
Запишите смешанное число в виде неправильной дроби.

Выделение целой части из неправильной дроби

В ответе не принято записывать неправильную дробь. Неправильную дробь предварительно заменяют либо равным ей натуральным числом (когда числитель делится нацело на знаменатель), либо проводят так называемое выделение целой части из неправильной дроби (когда числитель не делится нацело на знаменатель).

Выделение целой части из неправильной дроби – это замена дроби равным ей смешанным числом.

Осталось узнать, как можно выделить целую часть из неправильной дроби.

Докажем это утверждение.

Рассмотрим решение примера.

Выполним деление столбиком:

Таким образом, неправильная дробь 118/7 равна смешанному числу .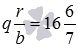

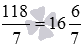
Источник

Как смешанное число перевести в неправильную дробь

Вопрос о том, как перевести смешанное число в неправильную дробь, возникает как при умножении и делении смешанных чисел, так и в качестве самостоятельного задания.

Чтобы смешанное число перевести в неправильную дробь, надо:

1) Целую часть умножить на знаменатель и к произведению прибавить числитель. Результат записать в числитель.

2) Знаменатель переписать без изменения.

С помощью схемы перевод смешанного числа в неправильную дробь можно изобразить так:

Теперь рассмотрим, как смешанное число перевести в неправильную дробь, на конкретных примерах.

А как целое число записать в виде неправильной дроби? Для этого достаточно представить его в виде дроби, числитель которой равен данному числу, а знаменатель — единица. С помощью схемы перевод целого числа в неправильную дробь можно изобразить так: