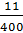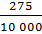Перевод обыкновенной дроби в десятичную видеоурок

Видеоурок «Десятичные дроби. Перевод обыкновенной дроби со знаменателем 10, 100, 1000 и т.д»

§ 1 Десятичные дроби

На этом уроке вы узнаете о понятии десятичной дроби, познакомитесь с ее историей, научитесь читать и записывать десятичные дроби, переводить обыкновенную дробь со знаменателем 10, 100,1000 и т.д. в десятичную и наоборот.

Итак, что же такое десятичная дробь? Оказывается, это форма записи обыкновенной дроби, у которой в знаменателе стоит 10, 100, 1000, 10000 и так далее, т.е. 1 с несколькими нулями. Сначала пишут целую часть, затем числитель дробной части, и целую часть от дробной, отделяют запятой.

Например, 12 целых 7 десятых записывают в виде 12,7. Другой пример: 8 целых 156 тысячных равно 8,156. А как же быть, если целая часть отсутствует? Т. е. дробь правильная? Тогда целую часть записывают в виде 0! Например, 17 сотых = 0,17.

§ 2 Перевод обыкновенной дроби со знаменателем 10, 100, 1000 и т.д. в десятичную дробь и наоборот

Внимание! Чтобы правильно записать десятичную дробь, числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе дробной части. Таким образом, дробь

Другой пример: как записать в десятичной записи дробь 3 миллионных?

Чтобы правильно читать десятичные дроби, необходимо запомнить, как называется каждый разряд в дробной части. На первом месте после запятой пишутся десятые доли, на втором – сотые, дальше тысячные, потом десятитысячные, затем стотысячные и т.д.

Например, вот это число (1234,5678 ) читается так: 1234 целых 5678 десятитысячных.

Теперь вы знаете, как переводить обыкновенную дробь в десятичную. А как же наоборот? Тоже достаточно просто! К примеру, десятичную дробь 1,5 прочитаем, как одна целая пять десятых и можно записать так:

дробь 1,05 читается как одна целая пять сотых и записывается как: 1

§ 3 История возникновения десятичных дробей

Оказывается, уже в древнем Китае пользовались десятичной системой мер и обозначали дробь словами, используя меры длины: чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.

Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков. Затем в 15 веке крупный ученый того времени Джемшид Гиясэддин аль – Каши впервые изложил учение о десятичных дробях, он ввел новую запись для десятичных дробей, когда целая и дробная части пишутся в одну строку и отделяются друг от друга либо вертикальной чертой, либо чернилами разных цветов. Примерно в то же время математики Европы пытались найти удобную запись десятичной дроби. В книге «Математический канон» французский математик Франсуа Виет в записи десятичной дроби дробную часть подчеркивал и записывал выше строки целой части числа. В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого. Запятая же в записи дробей впервые встречается в 1592г., а в 1617г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой. Современную запись десятичных Иоганн Кеплердробей, т.е. отделение целой части от дробной запятой, предложил Иоганн Кеплер. В странах, где говорят по английский и в настоящее время вместо запятой пишут точку.

Источник

Преобразование обыкновенной дроби в десятичную

Урок 16. Математика 6 класс ФГОС

Конспект урока «Преобразование обыкновенной дроби в десятичную»

Представим себе такую историю…

– Да как же они разгадываются? – задумался Саша.

– Что ты там не можешь разгадать? – поинтересовался Паша.

– Нам по математике задали разгадать ребус, по которому мы узнаем нашу следующую тему урока, – ответил Саша. — А я совсем не умею разгадывать ребусы.

– Не расстраивайся! – подбодрил друга Паша. – Я помогу тебе. Показывай свой ребус.

– Смотри, здесь почему-то нарисована часть клавиатуры с запятой, змея с равенством цифры и буквы, перевёрнутая коза с запятыми, сани тоже с равенством цифры и буквы, да ещё и буква «е», – стал перечислять увиденное Саша. – Совсем ничего не понять, что к чему?

– Саша, да это совсем лёгкий ребус, – возразил Паша. – Сейчас я тебе всё объясню, и мы вместе разгадаем слово. Запятые в ребусе означают, что из названия картинки нужно исключить столько букв, сколько стоит запятых. Если запятые стоят перед картинкой, то убираем буквы в начале слова, если после – в конце слова, – стал объяснять Паша. – Вот смотри, первая картинка в ребусе – это фрагмент клавиатуры с выделенными английскими буквами. Посмотрим, что за буквы будут соответствовать выделенным в русской раскладке.

– Это буквы «а», «п», «р», – вспомнил Саша.

– Правильно! – согласился Паша. – Обрати внимание: перед этой картинкой стоит одна запятая, значит, мы должны исключить первую букву. Тогда что останется?

– Убираем первую букву «а», – начал размышлять Саша. – Останутся только буквы «п», «р».

– Отлично! – поддержал друга Паша. – Идём дальше. Знак равенства, изображённый возле картинки, служит для обозначения замены одной из букв на другую. У тебя нарисована змея, а если быть точным, то кобра, а снизу равенство, указывающее, что нужно первую букву в названии картинки заменить на букву «е». Что за слово получится после замены?

– Была кобра, заменяем первую букву на «е», значит, у нас получится «еобра», – сказал Саша.

– Верно! – сказал Паша. – Перейдём к следующей картинке. Если картинка перевёрнута вверх ногами, это значит, что слово читается задом наперёд. Плюс у нас тут ещё нарисованы запятые. Значит, в перевёрнутом слове нужно исключить первую и последнюю буквы. Что тогда получится?

– У нас нарисована коза, – начал размышлять Саша. – Задом наперёд это слово читается так: «азок». Затем исключим первую и последнюю буквы. И останется у нас «зо».

– Молодец! – обрадовался за друга Паша. – Может, следующую картинку ты сможешь разгадать без моих подсказок?

– У нас нарисованы сани и рядом стоит равенство, показывающее, что первую букву нужно заменить на букву «в», – сказал Саша. – После замены получим слово «вани».

– Всё правильно! – согласился Паша. – А теперь из получившихся букв, слога и слов составь единое слово.

– Так, – начал Саша, – у нас есть буквы «п», «р», слово «еобра», слог «зо», слово «вани» и буква «е». Подумаем… Так это же «преобразование»!

– Молодец, Саша! – похвалил друга Паша. — Значит, на уроке математики вы будете знакомиться с преобразованиями!

– Интересно, что это за преобразования такие? – спросил Саша.

– А давай спросим у Мудряша, – предложил Паша. – Он точно расскажет.

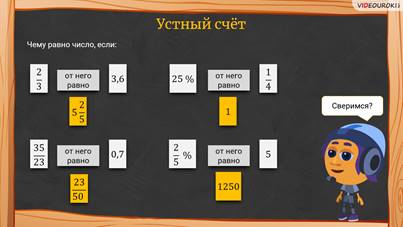
– Ребята, прежде чем я расскажу вам о преобразовании обыкновенной дроби в десятичную, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

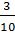
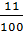
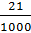
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Вы уже знаете, что для обыкновенных дробей со знаменателем 10, 100, 1000 и так далее существует «одноэтажная» форма записи – десятичные дроби. Вот, например, обыкновенную дробь мы можем записать в виде десятичной дроби следующим образом — 0,3, дробь можем переписать в виде десятичной как 0,11, а дробь как 0,021.

– А десятичные дроби можно преобразовать в обыкновенные, – сказали мальчишки.

– Верно! – согласился Мудряш. – Любую десятичную дробь можно преобразовать в обыкновенную дробь. Давайте преобразуем в обыкновенные дроби следующие десятичные дроби.

– Десятичную дробь 0,4 можно представить в виде обыкновенной дроби как 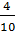, – начал Саша. – Можем сократить числитель и знаменатель дроби на 2. Тогда получится дробь .

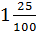
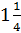
– А десятичную дробь 1,25 можно представить в виде смешанного числа , – продолжил Паша. – Дробную часть можем сократить на 25. Получим смешанное число . Затем запишем это число неправильной дробью .

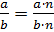
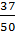
– Молодцы! – похвалил ребят Мудряш. – Также вы уже знакомы с основным свойством дроби . Напомню, что если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь. С помощью основного свойства дроби можно некоторые обыкновенные дроби преобразовать в десятичные. Например, преобразуем обыкновенные дроби и в десятичные дроби, используя основное свойство дроби.

– Числитель и знаменатель дроби можем умножить на 2, – начал Саша. – Получим дробь . А эту дробь мы спокойно можем записать десятичной 0,2, так как знаменатель равен 10.

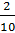
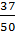
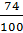
– Что касается второй дроби , – продолжил Паша, – то можем её числитель и знаменатель умножить на 2. Получим дробь . Её мы тоже можем представить в виде десятичной 0,74.

– Молодцы! – похвалил ребят Мудряш. — Мы сейчас с вами преобразовывали обыкновенные дроби в десятичные. Какой вывод можно сделать?

– Чтобы обыкновенную дробь представить в виде десятичной, нужно чтобы её знаменатель был равен 10, 100, 1000 и так далее, – сказали мальчишки.

– Верно! – сказал Мудряш. – Запомните! Чтобы несократимую дробь 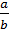преобразовать в десятичную, необходимо привести её к одному из знаменателей десять, сто, тысяча и так далее.

– А знаменатель можно выбирать любой из 10, 100, 1000 и так далее? – решили уточнить ребята. – Или существует какая-то особенность выбора?

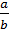
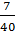
– Хороший вопрос! – сказал Мудряш. – Какой же из этих знаменателей выбрать? Обратите внимание, что при приведении несократимой дроби к новому знаменателю «старый» знаменатель является делителем «нового». Значит, знаменатель дроби обязательно должен быть делителем одного из чисел 10, 100, 1000 и так далее. Давайте преобразуем обыкновенную дробь в десятичную.

– Мне кажется я понял, как подбирать знаменатель, – сказал Паша. – Мы не сможем привести дробь 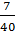к знаменателю 10, так как число 10 не делится нацело на 40.

– Ну тогда и к знаменателю 100 мы тоже не сможем привести эту дробь, – перебил друга Саша. – Ведь число 100 также не делится нацело на 40.

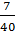
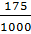
– Верно размышляете! – согласился Мудряш. – Числа 10 и 100 не подходят в качестве знаменателя. А вот число 1000 делится нацело на 40. Следовательно, обыкновенную дробь можно привести к знаменателю 1000. Для этого нужно числитель и знаменатель дроби умножить на 25. Получим дробь . А эту дробь легко записать в виде десятичной 0,175.

– Ты говорил, что любую десятичную дробь можно представить в виде обыкновенной, – сказали мальчишки. – Также и с обыкновенными? Любую обыкновенную дробь можно записать в виде десятичной?

– А вот тут дело обстоит сложнее – ответил Мудряш. – Не каждую обыкновенную дробь можно записать в виде десятичной. Вот, например, рассмотрим обыкновенную дробь . Исходя из признака делимости на 9, сразу можем заметить, что ни одно из чисел 10, 100, 1000 и так далее не делится нацело на 9. Значит, дробь преобразовать в десятичную не получится.

– А как тогда понять, какие несократимые дроби можно представить в виде десятичных? – спросили мальчишки.

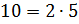
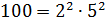
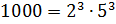
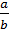
– Обратите внимание: каждое из чисел 10, 100, 1000 и так далее имеет только два простых делителя: это числа 2 и 5, – сказал Мудряш. – Число , , и так далее. Поэтому можем сделать такой вывод. Запомните! Несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя бэ на простые множители не содержит чисел, отличных от 2 и 5.

– Но ведь черту дроби можно рассматривать как знак деления, – заметил Паша. – А значит, мы можем числитель разделить на знаменатель и так перейти к десятичной записи числа.

– Верно подмечено! – согласился Мудряш. – Обыкновенные дроби можно преобразовать в десятичные и таким способом. Преобразуем, например, дробь одиннадцать шестнадцатых в десятичную. Дробь 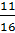запишем в виде частного числителя и знаменателя. Теперь выполним деление уголком. Получим 0,6875.

– Запомните! – сказал Мудряш. – Чтобы преобразовать обыкновенную дробь в десятичную, можно её числитель разделить на знаменатель.

– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.

Задание первое: какие из данных обыкновенных дробей можно преобразовать в десятичную: а) ; б) ; в) ; г) ?

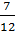
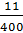
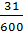
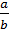
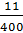
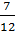
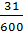
Решение: несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя бэ на простые множители не содержит чисел, отличных от 2 и 5. Исходя из этого, дроби и можно преобразовать в десятичные, так как разложения их знаменателей на простые множители не содержат чисел, отличных от 2 и 5. А вот дроби и не получится преобразовать в десятичные, так как разложения их знаменателей на простые множители содержат числа, отличные от 2 и 5.

Задание второе: преобразуйте в десятичную дробь: а) ; б) .

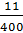
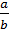
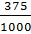
Решение: чтобы несократимую дробь преобразовать в десятичную, необходимо привести её к одному из знаменателей: 10, 100, 1000 и так далее. Первая дробь . Применим основное свойство и умножим числитель и знаменатель этой дроби на 125. Получим дробь . А теперь запишем эту дробь десятичной 0,375.

Следующая дробь — . Воспользуемся основным свойством дроби и умножим числитель и знаменатель этой дроби на 25. Получим дробь . Осталось записать эту дробь десятичной 0,0275.

Источник