Перевод градусов в радианы и обратно, формулы, примеры.
В этой статье мы установим связь между основными единицами измерения углов – градусами и радианами. Эта связь нам в итоге позволит осуществлять перевод градусов в радианы и обратно. Чтобы эти процессы не вызывали затруднений, мы получим формулу перевода градусов в радианы и формулу перехода от радианов к градусам, после чего подробно разберем решения примеров.
Навигация по странице.
Связь между градусами и радианами
Связь между градусами и радианами будет установлена, если будет известна и градусная и радианная мера какого-нибудь угла (с градусной и радианной мерой угла можно ознакомиться в разделе измерение углов).
Формулы перевода градусов в радианы и радианов в градусы
Из равенства вида 
, которое мы получили в предыдущем пункте, легко выводятся формулы перевода радианов в градусы и градусов в радианы.
Чтобы удовлетворить свое любопытство, вычислим приближенную величину угла в один радиан в градусах и величину угла в один градус в радианах. Для этого возьмем значение числа пи с точностью до десятитысячных, подставим его в формулы 
и 
, и проведем вычисления. Имеем 
и 
. Итак, один радиан приближенно равен 57 градусам, а один градус – 0,0175 радиана.
Наконец, от полученных соотношений и перейдем к формулам перевода радианов в градусы и наоборот, а также рассмотрим примеры применения этих формул.
Формула перевода радианов в градусы имеет вид: 
. Таким образом, если известна величина угла в радианах, то умножив ее на 180 и разделив на пи, получим величину этого угла в градусах.
Дан угол в 3,2 радиана. Какова мера этого угла в градусах?
Как перевести градусы в радианы
Нужна работа? Скачивай здесь
Бесплатно на любую тему
Градусы в радианы
Краткое описание
Угол — это два луча, выходящие из одной точки. Эта точка называется вершиной. Взяв за единицу измерения некий конкретный угол, можно определить величину любого угла, выяснив, сколько раз в нем укладывается такой единичный угол. При измерении угла исходят из двух его свойств:
Если ясно, о чем идет речь, вместо «величина угла» говорят просто «угол».
Равные углы с вершиной в центре окружности будут создавать на ней дуги одинаковой длины. Их сумма будет равняться сумме стягиваемых ими дуг. Поэтому единицы измерения углов можно задавать, указывая, какую часть окружности составляет соответствующая дуга.
В чем можно измерять угол
Наиболее распространены две единицы измерения:
Существуют еще такие единицы измерения, как град, равный 1/100 прямого угла, оборот, равный полному кругу, тысячная — \(\frac1<2\mathrm\pi\;\times\;1000>\) и румб — 1/32 полной окружности.
Связь между градусами и радианами
Мера угла
1/60 градуса — минута, обозначаемая знаком ‘. Секунду обозначают знаком », она составляет 1/3600 доли.
Формула соотношения
Длина дуги, высекаемой углом в a радиан на окружности радиуса R, вычисляется умножением a на R, а для единичной окружности длина дуги и величина угла совпадают.
Таким образом, связь радиан и градусов можно выразить формулой
Формулы перевода
Градусы в радианы
Осуществить переход от градусов к радианам можно по формуле
Радианы в градусы
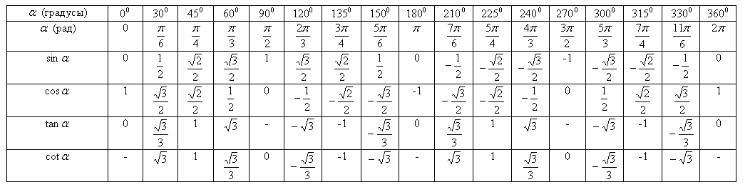
Таблица перевода градусов в радианы
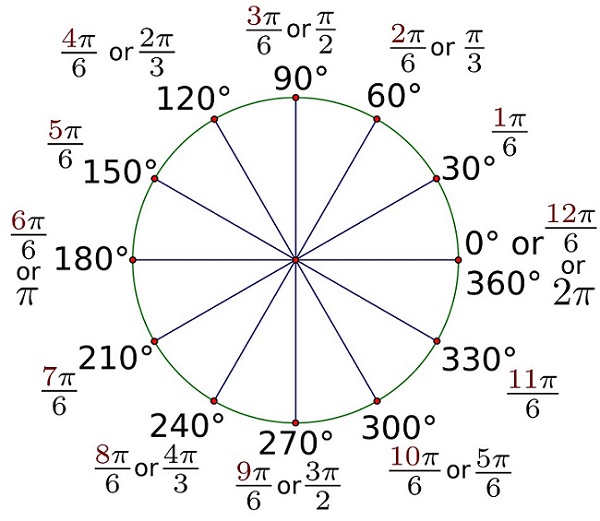
Соотношение двух систем измерения на окружности можно наглядно увидеть на схеме:
Но на практике, чтобы преобразовать одну величину измерения в другую, удобнее пользоваться таблицей:
Примеры расчета градусов и минут в радианы
Пример 1
Перевести 35 градусов в радианы.
Решение
Согласно формуле, нам нужно 35 умножить на число пи и разделить на 180.
Чтобы выполнить перевод минут и секунд, нужно сначала перевести их в градусы.
Пример 2
Решение
Воспользуемся формулой, подставив найденное значение:
Пример 3
Как перевести градусы в радианы: формулы перевода
С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки». Углы бывают разные: тупые, острые, прямые, развёрнутые, центральные, смежные. Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.
Что означают градус и радиан
Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние. Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления. Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.
Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир.
Кроме градусной меры для измерения углов применяют меру радианную. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным. Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.
Как перевести градусы в радианы и обратно
Мы знаем, что центральному углу в 360° соответствует вся окружность, длина которой вычисляется по известной формуле l=2•π•R. Разделим это выражение на R и получим: α= 2•π•R/R=2•π рад≈6,28 рад. Если взять какое-то угловое расстояние в A град., то его радианная мера α получится из пропорции: А/360°=α/(2•π). Решив это уравнение, получим формулу перевода градусов в радианы — α=(π/180°)•А, или формулу перевода радиан в градусы — А=(180°/π)•α. Из этих формул мы придём к следующим соотношениям:
Сколько составит 180 градусов в радианах и 90 градусов в радианах? Воспользовавшись полученными выше формулами, придём к таким соотношениям:
Итак, как правильно переводить градусную меру в радианную и обратно? В этом вам поможет следующее правило:
Чтобы найти число радиан, нужно градусную меру умножить на число π и поделить на 180. Чтобы найти число градусов, нужно радианную меру умножить на 180 и поделить на число π.
Примеры решения задач
Задача 1. Чему равна длина дуги окружности, если R=1 см, α=1 рад?
Решение. По формуле длины дуги найдём: l=R•α=1•1=1 см.
Задача 2. Сколько рад в 45°?
Решение. Используя правило, получим: α=45•π/180=π/4 рад.
Задача 3. Сколько град. в π² рад?
Решение. Используя правило, найдём: А=π²•180/π=180π град.≈565,5°.
Задача 4. Чему равен средний угловой размер лунного диска, если среднее расстояние до Луны равно R=384399 км, а диаметр самой Луны D=3476 км?
Решение. Если мысленно на Луну с Земли провести два луча, которые пройдут через крайние точки диаметра её диска, мы получим центральный угол, исходящий из глаз наблюдателя. Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α•R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05»≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.
Минуты и секунды
Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления. В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «’», а секунды — значком «»». Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения: