Перевод чисел из одной системы счисления в другую
Цели урока:
- повторить изученный материал по теме система счисления ;
- научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот;
- освоить принципы перевода чисел из одной системы в другую;
- развивать логическое мышление.
Ход урока
Вначале урока краткое повторение и проверка домашнего задания..
— В каком виде представлена числовая информация в памяти компьютера?
— Для чего используются системы счисления?
— Какие виды систем счисления вы знаете? Привести свои примеры.
— Чем отличаются позиционные системы от непозиционных?.
Цель нашего урока научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот. Но в начале мы рассмотрим, как можно
представить любое целое неотрицательное чисело:
В позиционных системах значение записи целого числа определяется по следующему правилу: пусть a na n-1a n-2…a 1a 0 — запись числа A, а i – цифры, тогда
A = a n·p n +a n-1·p n-1 +a n-2·p n-2 +. +a 1·p 1 + a0·p 0 (1),
где p — целое число большее 1, которое называется основанием системы счисления
Для того, чтобы при заданном p любое неотрицательное целое число можно было бы записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.
1) Десятичная система
число 5735 = 5·10 3 +7·10 2 +3·10 1 +8·10 0
2) Троичная система
число 2013 = 2·3 2 +0·3 1 +1·3 0
Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.
Представление отрицательных и дробных чисел:
Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘. Для отделения целой части числа от дробной используется запятая. Значение записи a na n-1a n-2…a 1a 0, a -1 a -2…a m-2 a m-1a m числа A определяется по формуле, являющейся обобщением формулы (1):
A = an·p n +a n-1·p n-1 +a n-2·p n-2 +…+a1·p 1 +a0·p 0 +a-1·p -1 +a -2·p -2 +…+am-2·p –(m–2 )+am–1·p –(m–1 )+amp –m (2),
75,6 = 7·10 1 +5·10 0 +6·10 –1
–2,3145 = –(2·5 0 +3·5 –1 +1·5 –2 +4·5 –3 )
Перевод чисел из произвольной системы счисления в десятичную:
Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.
Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.
Перевод чисел из десятичной системы счисления в произвольную.
Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором. Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что 23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·8 1 +7·8 0 +4·8 –1 =27,48. Понятно, что не всегда ответ столь очевиден. В общем случае применяется способ перевода отдельно целой и дробной частей числа.
Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):
1. Найдем частное и остаток от деления числа на p. Остаток будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.
2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.
Замечание 1. Цифры ai в записи числа нумеруются справа налево.
Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.
Перевести число 165 в семеричную систему счисления.
165:7 = 23 (остаток 4) => a0 = 4
23:7 = 3 (остаток 2) => a1 = 2
3:7 = 0 (остаток 3) => a2 = 3
Выполнив проверку по формуле (1), убедимся в правильности перевода:
3247=3·7 2 +2·7 1 +4·7 0 =3·49+2·7+4 = 147+14+4 = 165.
Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):
1. Умножим дробную часть числа на p.
2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.
Замечание 1. Цифры am в записи числа располагаются слева направо в порядке возрастания абсолютного значения m.
Замечание 2. Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.
Перевести число 0,625 в двоичную систему счисления.
0,625·2 = 1,25 (целая часть 1) => a-1 =1
0,25·2 = 0,5 (целая часть 0) => a-2 = 0
0,5·2 = 1,00 (целая часть 1) => a-3 = 1
Итак, 0,62510 = 0,1012
Выполнив проверку по формуле (2), убедимся в правильности перевода:
0,1012=1·2 -1 +0·2- 2 +1·2 -3 =1/2+1/8 = 0,5+0,125 = 0,625.
Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.
0,165·4 = 0,66 (целая часть 0) => a-1=0
0,66·4 = 2,64 (целая часть 2) => a-2= 2
0,64·4 = 2,56 (целая часть 2) => a-3= 2
0,56·4 = 2,24 (целая часть 2) => a-4= 2
Итак, 0,16510 ” 0,02224
Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:
0,02224 = 0·4 -1 +2·4 -2 +2·4 -3 +2·4 -4 = 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625
|0,1640625–0,165| = 0,00094 4 ). Сгруппируем цифры по четыре, дописав, слева и справа нужное количество нулей
и, сверяясь с таблицей, получим: 1A9554,C16
Вывод:
В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.
А человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр. Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.
Записываем задание на дом:
а) Запишите дату рождения всех членов вашей семьи в различных системах счисления.
б) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
Как перевести число из двоичной системы в десятичную
В задачах по теме Системы счисления часто требуется перевести число из двоичной в десятичную систему счисления. Чтобы выполнить такое задание, нужно воспользоваться алгоритмом перевода числа из двоичной системы счисления в десятичную.
Алгоритм перевода из двоичной системы в десятичную
- Пронумеровать разряды двоичного числа справа налево, начиная с нуля.
- Умножить каждый ненулевой разряд на 2 в степени его номера и сложить результаты.
Онлайн калькулятор перевода чисел из одной системы счисления в любую другую
Перевести число 1111001102 из двоичной системы в десятичную.
Нумеруем разряды числа справа налево, начиная с нуля:
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
И вычисляем результат:
1111001102 = 1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 2 + 1 ⋅ 2 1 = 256 + 128 + 64 + 32 + 4 + 2 = 48610
Перевести число 1010001112 из двоичной системы в десятичную.
Нумеруем разряды числа справа налево:
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
И вычисляем результат:
1010001112 = 1 ⋅ 2 8 + 1 ⋅ 2 6 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 256 + 64 + 4 + 2 + 1 = 32710
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2020 Все калькуляторы online
Копирование материалов запрещено
Системное администрирование и мониторинг Linux/Windows серверов и видео CDN
Статьи по настройке и администрированию Windows/Linux систем
Перевод чисел в различные системы счислений
Когда занимаешься настройками сетей различного масштаба и каждый день сталкиваешься с вычислениями – то такого рода шпаргалки заводить не обязательно, все и так делается на безусловном рефлексе. Но когда в сетях ковыряешься очень редко, то не всегда вспомнишь какая там маска в десятичной форме для префикса 21 или же какой адрес сети при этом же префиксе. В связи с этим я и решил написать несколько маленьких статей-шпаргалок по переводом чисел в различные системы счислений, сетевым адресам, маскам и т.п. В это части пойдет речь о переводи чисел в различные системы счислений.
1. Системы счислений
Когда вы занимаетесь чем-то связанным с компьютерными сетями и ИТ, вы по любому столкнетесь с этим понятием. И как толковый ИТ-шник вам нужно разбираться в этом хотя бы чу-чуть даже если на практике вы это будете применять очень редко.
Рассмотрим перевод каждой цифры из IP-адреса 98.251.16.138 в следующие системы счислений:
- Двоичная
- Восьмеричная
- Десятичная
- Шестнадцатеричная
1.1 Десятичная
Так как цифры записаны в десятичной, перевод с десятичной в десятичную пропустим 🙂
1.1.1 Десятичная → Двоичная
Как мы знаем двоичная система счисления используется практически во всех современных компьютерах и многих других вычислительных устройствах. Система очень проста – у нас есть только 0 и 1.
Для преобразования числа с десятиной в двоичную форму нужно использовать деление по модулю 2 (т.е. целочисленное деление на 2) в результате чего мы всегда будем иметь в остатке либо 1, либо 0. При этом результат записываем справа налево. Пример все поставит на свои места:
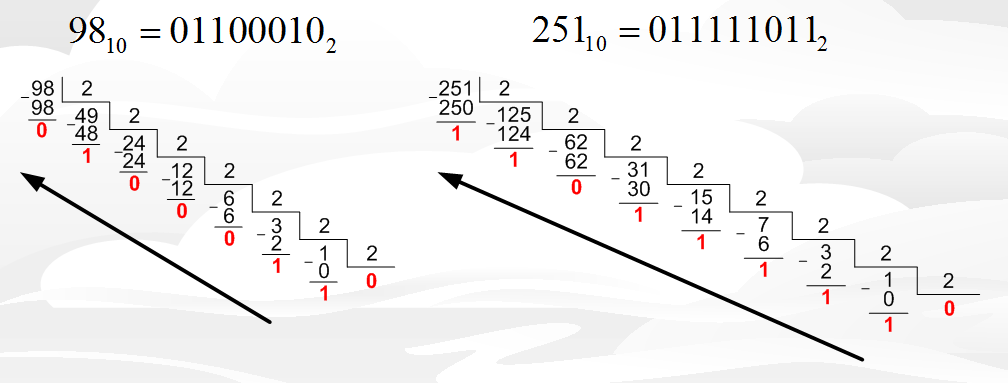
Рисунок 1.1 – Перевод чисел из десятичной в двоичную систему
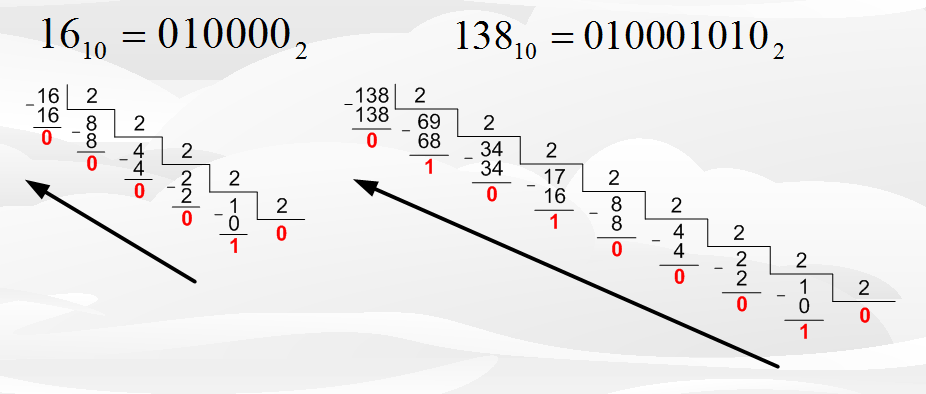
Рисунок 1.2 – Перевод чисел из десятичной в двоичную систему
Опишу деление числа 98. Мы делим 98 на 2, в результате имеем 49 и остаток 0. Далее продолжаем деление и делим 49 на 2, в результате имеем 24 с остатком 1. И таким же образом добираемся до 1-ки или 0-ка в делимом. Затем результат записываем справа налево.
1.1.2 Десятичная → Восьмеричная
Восьмеричная система – это целочисленная система счисления с основанием 8. Т.е. все числа в ней представлены диапазоном 0 – 7 и для перевода с десятичной системы нужно использовать деление по модулю 8.
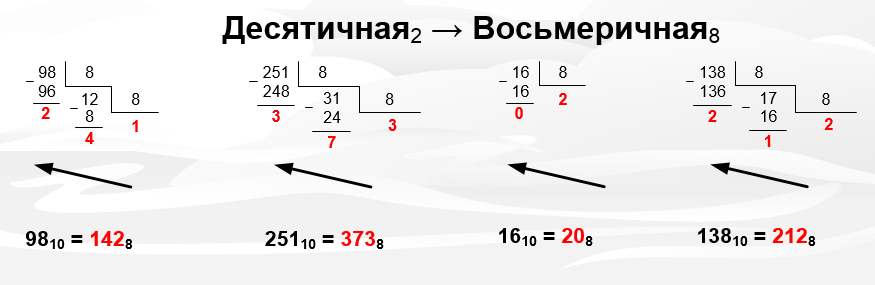
Рисунок 1.3 – Перевод чисел из десятичной в восьмеричную систему
Деление аналогично 2-чной системе.
1.1.3 Десятичная → Шестнадцатеричная
Шестнадцатеричная система почти полностью вытеснила восьмеричную систему. У нее основание 16, но используются десятичные цифры от 0 до 9 + латинские буквы от A(число 10) до F(число 15). С ней вы сталкиваетесь каждый раз, когда проверяете настройки сетевого адаптера — это МАС-адрес. Так же, когда используется IPv6.
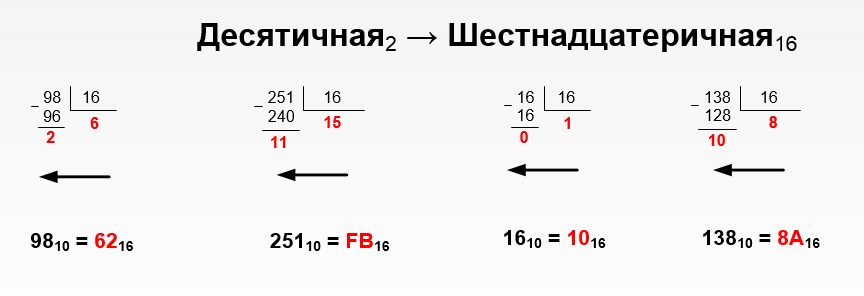
Рисунок 1.4 – Перевод чисел из десятичной в шестнадцатеричную систему
1.2 Двоичная
В предыдущем примере мы перевели все десятичные числа в другие системы счислений, одна из которых двоичная. Теперь переведем каждое число с двоичной формы.
1.2.1 Двоичная → Десятичная
Для перевода чисел с двоичной формы в десятичную нужно знать два нюанса. Первый – у каждого нолика и единички есть множитель 2 в n-й степени, при котором n увеличивается справа налево ровно на единичку. Второй – после перемножения все числа нужно сложить и мы получим число в десятичной форме. В итого у нас будет формула такого вида:
Где,
D – это число в десятичной форме, которое мы ищем;
n – количество символов в двоичном числе;
a – число в двоичной форме на n-й позиции (т.е. первый символ, второй, и т.п.);
p – коэффициент, равный 2,8 или 16 в степени n (в зависимости от системы счисления)
К примеру возьмем число 110102. Смотрим на формулу и записываем:
- Число состоит из 5 символов (n=5)
D = (1 × 2 5-1 ) + (1 × 2 5-2 ) + (0 × 2 5-3 ) + (1 × 2 5-4 ) + (0 × 2 5-5 ) = 16 + 8 + 0 + 2 + 0 = 2610
Кто привык записывать справа на лево, форму будет выглядеть так:
D = (0 × 2 5-5 ) + (1 × 2 5-4 ) + (0 × 2 5-3 ) + (1 × 2 5-2 ) + (1 × 2 5-1 ) = 0 + 2 + 0 + 8 + 16 = 2610
Но, как мы знаем, от перестановки слагаемых сумма не меняется. Давайте теперь переведем наши числа в десятичную форму.
Рисунок 1.5 – Перевод чисел из двоичной в десятичную систему
1.2.2 Двоичная → Восьмеричная
При переводе нам нужно двоичное число разбить на группы по три символа справа налево. Если последняя группа не состоит из трех символов, то мы просто возмещаем недостающие биты ноликами. К примеру:
10101001 = 0 10 101 001
1011100 = 00 1 011 100
Каждая группа битов – это одно из восьмеричных чисел. Чтобы узнать какое, нужно использовать написанную выше формулу 1.2.1 для каждой группы битов. В результате мы получим.
Рисунок 1.6 – Перевод чисел из двоичной в восьмеричную систему
1.2.3 Двоичная → Шестнадцатеричная
Здесь нам нужно двоичное число разбивать на группы по четыре символа справа налево с последующим дополнением недостающих битов группы ноликами, как писалось выше. Если последняя группа состоит из ноликов, то их нужно игнорировать.
110101011 = 000 1 1010 1011
1011100 = 0 101 1100
001010000 = 00 0101 0000 = 0101 0000
Каждая группа битов – это одно из шестнадцатеричных чисел. Используем формулу 1.2.1 для каждой группы битов.
Рисунок 1.7 – Перевод чисел из двоичной в шестнадцатеричную систему
1.3 Восьмеричная
В этой системе у нас могут возникнуть сложности только при переводе в 16-ричную систему, так как остальной перевод проходит гладко.
1.3.1 Восьмеричная → Двоичная
Каждое число в восьмеричной системе – это группа из трех битов в двоичной системе, как писалось выше. Для перевода нам нужно воспользоваться табличкой-шпаргалкой:
Рисунок 1.8 – Шпора по переводу чисел из восьмеричной системы
Используя эту табличку переведем наши числа в двоичную систему.
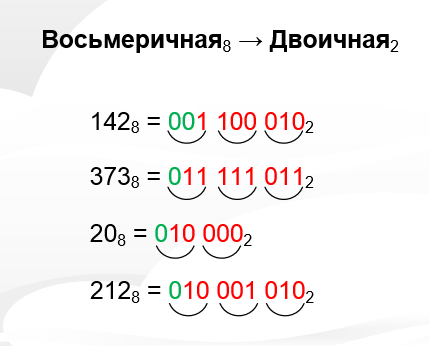
Рисунок 1.9 – Перевод чисел из восьмеричной в двоичную систему
Немного опишу вывод. Первое число у нас 142, значит будет три группы по три бита в каждой. Юзаем шпору и видим, что цифра 1 это 001, цифра 4 это 100 и цифра 2 это 010. В результате имеем число 001100010.
1.3.2 Восьмеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 8 (т.е. p=8). В результате имеем
Рисунок 1.10 – Перевод чисел из восьмеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 3 символов (n=3)
В результате имеем:
D = (1 × 8 3-1 ) + (4 × 8 3-2 ) + (2 × 8 3-3 ) = 64 + 32 + 2 = 9810
1.3.3 Восьмеричная → Шестнадцатеричная
Как писалось раньше, для перевода нам нужно сначала перевести числа в двоичную систему, потом с двоичной в шестнадцатеричную, поделив на группы по 4-ре бита. Можно использовать следующею шпору.
Рисунок 1.11 – Шпора по переводу чисел из шестнадцатеричной системы
Эта табличка поможет перевести из двоичной в шестнадцатеричную систему. Теперь переведем наши числа.
Рисунок 1.12 – Перевод чисел из восьмеричной в шестнадцатеричную систему
1.4 Шестнадцатеричная
В этой системе та же проблема, при переводе в восьмеричную. Но об этом позже.
1.4.1 Шестнадцатеричная → Двоичная
Каждое число в шестнадцатеричной системе – это группа из четырех битов в двоичной системе, как писалось выше. Для перевода нам можно воспользоваться табличкой-шпаргалкой, которая находиться выше. В результате:
Рисунок 1.13 – Перевод чисел из шестнадцатеричной в двоичную систему
Возьмем первое число – 62. Используя табличку (рис. 1.11) мы видим, что 6 это 0110, 2 это 0010, в результате имеем число 01100010.
1.4.2 Шестнадцатеричная → Десятичная
Здесь мы используем формулу 1.2.1 только с коэффициентом 16 (т.е. p=16). В результате имеем
Рисунок 1.14 – Перевод чисел из шестнадцатеричной в десятеричную систему
Возьмем первое число. Исходя из формулы 1.2.1:
- Число состоит из 2 символов (n=2)
В результате имеем.
D = (6 × 16 2-1 ) + (2 × 16 2-2 ) = 96 + 2 = 9810
1.4.3 Шестнадцатеричная → Восьмеричная
Для перевода в восьмеричную систему нужно сначала перевести в двоичную, затем разбить на группы по 3-и бита и воспользоваться табличкой (рис. 1.8). В результате:
Рисунок 1.15 – Перевод чисел из шестнадцатеричной в восьмеричную систему
В следующей статье пойдет речь о IP-адресах, масках и сетях.