Представление отрицательных чисел в двоичной системе счисления
Положительные числа нами были рассмотрены ранее. Рассмотрим способы представления отрицательных чисел в двоичном коде. Существует несколько способов такого представления. Мы рассмотрим три:
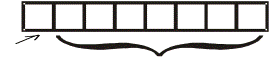
1. прямой код (в этом случае в двоичном числе выделяется бит-знака — старший бит). Рассмотрим однобайтное (8 бит) двоичное число со знаком.
Старший бит младший бит
Рисунок 2.5 — Представление однобайтных чисел со знаком
Если бит-знак равен 0, то число считается положительным, а если бит-знак равен 1 = отрицательным.
Недостатком прямого кода является невозможность выполнения арифметических операций.
Рассмотрим сложение: 12+(-12)=0
Как видим в результате сложения получились число -24, что не равно 0.
2. смещенный код (аналогично прямому коду двоичное число, в смещенном число разделяется на бит-знак и мантиссу, причем, если бит-знак равен 0, то это число отрицательное, а если бит-знак равен 1 — положительное).
Числа здесь представляются так:
| Число в смещенном коде | Двоичный код | Число без знака |
| ………. | ……… | ..……. |
| -1 | ||
| ………. | ………. | ……… |
| -127 | ||
| -128 |
Достоинством данной системы является то, что в ней выполняются арифметические операции, правда с учетом коррекции результата. А недостатком является то, что 0 соответствует числу 128.
Рассмотрим сложение: 12+(-12)=0
Как видим, в результате операции получилось число 256. Ограничив предел рассмотрения одним байтом, получим 00000000, к этому результату надо прибавить смещение 128.
Рассмотрим сложение: 12+(-13)=0
Как видим, и в данном случае к результату необходимо прибавить 128 и ограничить рассмотрение одним байтом.
3. дополнительный код (это наиболее широко используемый код для представления отрицательных чисел). В нем в числе также выделяется бит-знак в старшем разряде. В дополнительном коде ноль в старшем разряде соответствует положительным числам, а единица — отрицательным числам, но при этом положительные числа представляются как обычно, а отрицательные — в виде записи дополнительного кода.
Рассмотрим порядок перевода числа -9 из десятичной системы в дополнительный код:
1. запишем число без знака: 9;
2. преобразуем число в двоичный код: 00001001;
3. получим обратный код: 11110110;
4. прибавим 00000001 и получим: 11110111.
Если результат операции представлен в дополнительном коде, то для перевода его в десятичный вид используем нижеследующую процедуру
1. запишем дополнительный код: 11110111;
2. получим обратный код: 00001000;
3. прибавим 00000001: 00001001;
4. преобразуем число в десятичный код: -9
Знак минус мы добавили, так как знаем, что наше исходное число в дополнительном коде отрицательное (старший бит равен 1)
Рассмотрим таблицу соответствия чисел представленных в дополнительном коде.
| Число со знаком | Двоичный код | Число без знака |
| +127 | ||
| ………………………. | ………………………… | ………………………… |
| +2 | ||
| +1 | ||
| +0 | ||
| -1 | ||
| -2 | ||
| -3 | ||
| ………………………. | ………………………… | ………………………… |
| -128 |
В дополнительном коде сохраняются все правила выполнения арифметических операций.
Дата добавления: 2014-01-07 ; Просмотров: 9019 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/747/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
А это все для удобной работы со знаками. Поскольку я все люблю понимать на примерах, рассказывать я тоже буду на примерах. Итак, предположим, что у нас 4 разряда для работы с двоичными числами. Представить таким образом можно 16 чисел — 0, 1, . 15
00 — 0000
.
15 — 1111
Но если нет знака, убогая получается арифметика. Нужно вводить знак. Чтобы никого не обидеть, половину диапазона отдадим положительным числам (8 чисел), половину — отрицательным (тоже 8 чисел). Ноль, что отличает машинную арифметику от обычной, мы отнесем в положительные числа (в обычной арифметике у нуля нет знака, если не ошибаюсь). Итого, в положительные числа попадают 0. 7, а в отрицательные -1, . -8.
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
Вот для их представления как раз и используется дополнительный код.
То есть, -7 в дополнительном коде получается так
прямой код 7 = 0111
обратный код 7 = 1000
дополнительный код 7 = 1001
Обратим внимание на то, что прямой код 1001 представляет число 9, которое отстоит от числа -7 ровно на 16, или .
Или, что тоже самое, дополнительный код числа «дополняет» прямой код до , т.е. 7+9=16
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.