Обратный польский калькулятор
Попробуем написать синтаксический анализатор математических выражений, который переводит их в обратную польскую запись и вычисляет результат. Например, такое выражение:
в обратной польской записи будет выглядеть так:
Для чего нужна такая запись? Во-первых, её можно использовать на некоторых реальных калькуляторах. В ней отсутствуют скобки, и поэтому порядок введения операций в калькулятор последовательный (не требует запоминания промежуточных результатов и т.п.) Во-вторых, она очень просто обрабатывается алгоритмически и потому подходит для различных программных реализаций. Алгоритм действительно очень простой и работает на стеке:
- Получить очередную часть выражения
- Если это число, положить его в стек
- Если это операция, то достать из стека 2 числа, сделать с ними эту операцию, и результат положить назад в стек.
После обработки всего выражения результат будет лежать на вершине стека.
Итак, начнём с написания синтаксического анализатора для исходных выражений. Требуется на основании входной строки получить структуру, в которой будут сохранены уже отдельные операнды и операции для дальнейшего использования. Необходимо учитывать следующие условия:
- Умножение и деление имеют приоритет над сложением и вычитанием
- Скобки имеют приоритет над любыми операциями
Если вы приступаете к этой задаче с нуля, в голове может не быть ясности, и это нормально. Совет здесь только один – не пишите сразу готовый анализатор, просто начните хоть с чего-то, хотя бы с перебора символов в строке и с определения, чем они являются. После этого начнут появляться различные мысли.
Чтобы пока не усложнять код, будем считать, что все числа – целые и положительные. Значит, исходное выражение состоит только из цифр 0..9, скобок () и знаков +-*/.
Допустим, мы движемся по строке посимвольно и смотрим, чему равен текущий символ. Если это цифра, значит мы в данный момент читаем число. Но число может состоять из нескольких цифр. Значит, надо аккумулировать прочитанные цифры в одной переменной.
А если мы встретим скобку или знак операции? Это не цифра, поэтому мы будем знать, что число закончилось (или вообще не начиналось). Аккумулированный до этого результат (если он не пустой) станет финальным числом, мы сохраним его и будем готовы аккумулировать следующее.
А если это не цифра, то что? Открывающая или закрывающая скобка? Пока непонятно, что с ней делать, просто пропустим её. Это знак операции? Вычислять пока ничего не надо, поэтому здесь всё просто – сохраним знак как часть выражения, так же как мы сохранили число.
Набросаем простейший код на Питоне:
И для строки ‘128*(3+64)-1’ мы получаем результат:
То есть это список, где уже «раскиданы» конкретные числа и конкретные операции.
Код пока ещё ОЧЕНЬ сырой. В частности, в нём нет никакой обработки ошибок. Я делаю так исключительно для того, чтобы не отвлекаться от главного.
Из полученного списка уже можно было бы сформировать обратную польскую запись, но не хватает информации о приоритете операций. Сначала должна выполниться операция «+», затем «*», затем «-«. В обратной польской записи это должно выглядеть так:
Короче говоря, нужно вместе со знаками операций сохранять и их приоритет. Сделать это довольно просто: мы и так знаем, что ‘*’ и ‘/’ более приоритетны, чем ‘+’ и ‘-‘, но есть ещё скобки. Мы их пока пропускали, но теперь обработаем так: каждая открывающая скобка поднимает базовый приоритет, а каждая закрывающая снижает его.
Пусть операции ‘+’ и ‘-‘ имеют приоритет 0, а операции ‘*’ и ‘/’ приоритет 1. Тогда реальный приоритет каждой операции будет складываться из её собственного приоритета и базового приоритета. Увеличение базового приоритета должно происходить на шаг больший, чем максимальный приоритет операции. То есть у наших операций максимальный приоритет это 1. Значит, базовый приоритет должен увеличиваться минимум на 2 с каждой открывающей скобкой. Тогда любые операции внутри скобок будут иметь заведомо больший приоритет, чем вне их.
И теперь мы получили такой результат:
То есть там, где сохранялся просто знак, теперь сохраняется мини-список со знаком и приоритетом. Приоритеты уже правильные. Если мы выберем операции в нужном порядке (от максимального приоритета к минимальному), то уже сможем составить обратную польскую запись.
Но как перебрать их в нужном порядке? Искать в списке операцию с максимальным приоритетом, обрабатывать её, потом опять искать. Можно, но это всё как-то печально.
Давайте сделаем чуть проще. Будем отслеживать максимальный приоритет непосредственно при разборе строки и сохраним его в переменной.
В списке результатов первыми нужно обработать операции с максимальным приоритетом. То есть мы пройдём по списку, выберем все операции, у которых приоритет равен максимальному, и обработаем их.
Затем уменьшим максимальный приоритет, ещё раз пройдём по списку результатов, и обработаем все операции с этим приоритетом. Потом опять уменьшим приоритет и т.д., пока не обработаем все операции.
Хорошо, а как именно мы будем обрабатывать операции? Напомню расклад:
Мы начинаем с операции ‘+’ (приоритет 2). Слева и справа от неё стоят два числа: 3 и 64. Так как у этой операции максимальный приоритет, то числа «притягиваются» именно к ней. Для переноса в польскую нотацию мы запишем эти два числа и операцию:
Весь этот результат, то есть ‘3 64 +’ целиком, мы поместим обратно в список вместо трёх элементов: (3, ‘+’, 64), и удалим лишние элементы. Там, где были три элемента «3, +, 64», теперь один элемент, который содержит в себе всю эту операцию.
Следующая операция – ‘*’ (приоритет 1). Слева от неё число 128, а справа – та самая операция, которую мы обработали на предыдущем шаге. Делаем то же самое, то есть переписываем левую часть, правую часть и знак:
И вставляем то, что получилось, на старое место, удаляя лишние элементы. Теперь список имеет вид:
Осталось обработать операцию ‘-‘ (приоритет 0). Слева от неё – операция, полученная на предыдущем шаге, справа – число 1. Повторяем запись «лево-право-знак»:
И помещаем обратно в список, удаляя лишние элементы:
Всё, в списке не осталось больше знаков операций и остался один элемент, который и является обратной польской записью.
Допишем код, добавив в него запоминание максимального приоритета и обход списка с генерацией польской записи ( ссылка ):
- В целях экономии места был написан примитивный код, который сломается, если в исходном выражении что-то будет неправильно. Добавление различных условий и проверок сделает код замусоренным. Но мы не откажемся от проверок, а просто сделаем более элегантное решение с использованием ООП .
- Обработка списка с операциями это, если приглядеться, построение дерева в неявном виде. Мы могли бы строить дерево более наглядно, но опять же это заняло бы больше места. Освоившись с базовым решением, мы также сделаем вариант с явным деревом в ООП.
Обратная польская запись: алгоритм, методы и примеры
Обратная польская запись некогда составляла основу мира компьютерного программиста. Сегодня она уже не так хорошо известна. Поэтому шуточная иллюстрация, изображающая «обратную» польскую колбасу за пределами булочки, все еще может оказаться непонятой некоторыми хорошо осведомленными программистами. Не очень хорошо объяснять шутку, но в данном случае это будет в полной мере оправдано.
Инфиксная запись
Все программисты и большинство школьников знакомы с использованием операторов. Например, в выражении х + у для суммирования значений переменных х и у использован знак сложения. Менее известно то, что это заимствованное из математики обозначение, называемое инфиксной нотацией, на самом деле представляет большую проблему для машин. Такой оператор принимает в качестве входных два значения, записанные слева и справа от него. В программировании использовать нотацию со знаками операций необязательно. Например, х + у можно записать в виде функции сложить (х, у), в которую компилятор в конце концов и преобразует инфиксную нотацию. Однако все знают математику слишком хорошо, чтобы не использовать арифметические выражения, которые образуют своего рода внутренний мини-язык почти в каждом языке программирования.
Трансляторы формул
Первый действительно успешный язык программирования Fortran стал таким в основном потому, что арифметические выражения (т. е. формулы) в нем преобразовывались (транслировались) в код, откуда и произошло его название – FORmula TRANslation. До этого их приходилось записывать, например, в виде функций сложить (а, умножить (b, c)). В Коболе проблема реализации автоматического преобразования формул считалась очень трудной, поскольку программистам приходилось писать такие вещи, как Add A To B Mutliply By C.
Что не так с инфиксом?
Проблема заключается в том, что операторы обладают такими свойствами, как приоритет и ассоциативность. Из-за этого определение функции инфикса становится нетривиальной задачей. Например, приоритет умножения выше, чем сложения или вычитания, и это означает, что выражение 2 + 3 * 4 не равно сумме 2 и 3, умноженной на 4, как это бы было при выполнении операторов слева направо. На самом деле следует умножить 3 на 4 и прибавить 2. Этот пример иллюстрирует, что вычисление инфиксного выражения часто требует изменения порядка операторов и их операндов. Кроме того, приходится использовать скобки, чтобы нотация выглядела более ясно. Например, (2 + 3) * (4 + 5) нельзя записать без скобок, потому что 2 + 3 * 4 + 5 означает, что необходимо умножить 3 на 4 и добавить 2 и 5.
Порядок, в котором необходимо вычислять операторы, требует долгого запоминания. Из-за этого школьники, начинающие изучать арифметику, часто получают неправильные результаты, даже если фактически операции выполняются правильно. Необходимо учить порядок действия операторов наизусть. Сперва должны выполняться действия в скобках, затем умножение и деление и, наконец, сложение и вычитание. Но есть и другие способы записи математических выражений, поскольку инфиксная нотация является всего лишь одним из возможных «малых языков», которые можно добавить к большему.
Префиксная и постфиксная нотация
Двумя наиболее известными альтернативными вариантами является запись оператора до или после его операндов. Они известны как префиксная и постфиксная нотации. Логик Ян Лукасевич придумал первую из них в 1920-е годы. Он жил в Польше, поэтому запись называют польской. Постфиксный вариант, соответственно, получил название обратной польской нотации (ОПН). Единственная разница между этими двумя методами состоит в направлении, в котором следует читать запись (слева направо или справа налево), поэтому достаточно подробно рассмотреть только один из них. В ОПН оператор записывается после его операндов. Так, выражение АВ + представляет собой пример обратной польской записи для A + B.
Неограниченное число операндов
Непосредственным преимуществом нотации является то, что она обобщается n-адическим оператором, а инфиксная нотация на самом деле работает только с двумя операндами, т. е. по своей природе подходит только для бинарных операций. Так, например, ABC @ является обратным польским выражением с использованием триадического знака, который находит максимальное значение из A, B и C. В этом случае оператор действует на 3 операнда слева от себя и соответствует вызову функции @ (A, В, С). Если попытаться записать символ @ в качестве инфиксного, например A @ BC или что-то подобное, то становится понятно, что это попросту не работает.
Приоритет задается порядком
Обратная польская запись имеет еще одно преимущество в том, что приоритет операторов может быть представлен порядком их появления. При этом никогда не понадобятся скобки, хотя они могут быть включены в качестве знаков операций, чтобы облегчить конвертацию с инфиксной нотацией. Например, АВ + С * – однозначный эквивалент (А + В) * С, так как умножение не может быть вычислено, пока не будет выполнено сложение, которое дает второй операнд для операции умножения. То есть если вычисляется AB + C * по одному оператору за раз, то получится A B + C * -> (A B +) * C -> (A+B)*C.
Алгоритм вычисления
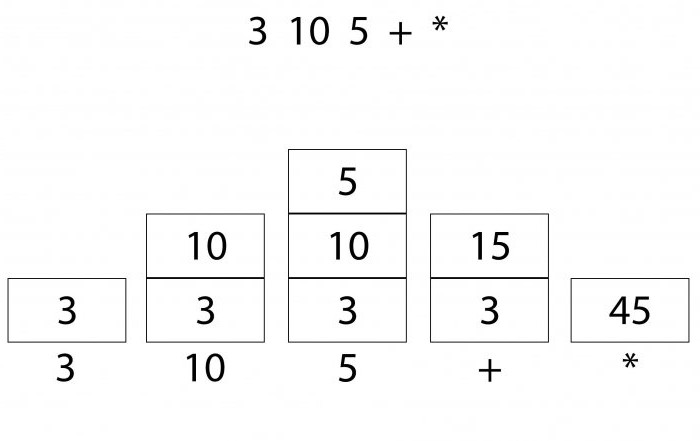
В ОПН оператор выглядит так же, как функция, которая принимает в качестве аргументов два значения, записанные слева от нее. Кроме того, это естественная нотация для использования в языках программирования, поскольку ход ее вычислений соответствует стековым операциям и необходимость в синтаксическом анализе отпадает. Например, в ОПН выражение 5 + 6 * 7 будет выглядеть как 5, 6, 7 *, +, и оно может быть вычислено просто путем сканирования слева направо и записи значений в стек. Каждый раз, когда встречается знак операции, выбираются 2 верхних элемента из машинной памяти, применяется оператор и результат возвращается в память. При достижении конца выражения результат вычислений окажется в вершине стека.
- S = () 5, 6, 7, *, + поместить 5 в стек.
- S = (5) 6, 7, *, + поместить 6 в стек.
- S = (5, 6) 7, *, + поместить 7 в стек.
- S = (5, 6, 7) *, + выбрать 2 значения из стека, применить * и поместить результат в стек.
- S = (5, 6 * 7) = (5, 42) + выбрать 2 значения из стека, применить + и поместить результат в стек.
- S = (5 + 42) = (47) вычисление завершено, результат находится в вершине стека.
Этот алгоритм обратной польской записи можно проверять многократно, но каждый раз он будет работать, независимо от того, насколько сложным является арифметическое выражение.
ОПН и стеки тесно связаны между собой. Приведенный пример наглядно демонстрирует, как можно использовать память, чтобы вычислить значение в обратной польской нотации. Менее очевидно, что можно использовать стек, преобразовав стандартные инфиксные выражения в ОПН.
Примеры на языках программирования
На языке Паскаль обратная польская запись реализуется примерно так (приведена часть программы).
Для считывания чисел и операторов в цикле вызывается процедура, которая определяет, является ли токен числом или знаком операции. В первом случае значение записывается в стек, а во втором над двумя верхними числами стека выполняется соответствующие действие и результат сохраняется.
if с in [‘+’, ‘-‘, ‘*’, ‘/’] then begin
if eoln then cn := ‘ ‘ else read(cn);
‘+’: toktype := add; ‘-‘: toktype := sub;
‘*’: toktype := mul; ‘/’: toktype := div
if с = ‘-‘ then sgn := -1 else error := с <> ‘+’;
if (not error) and (toktype = num) then getnumber;
if toktype <> num then begin
add: z := х+у; sub: z := х-у; mul: z := х*у; div: z := х/у
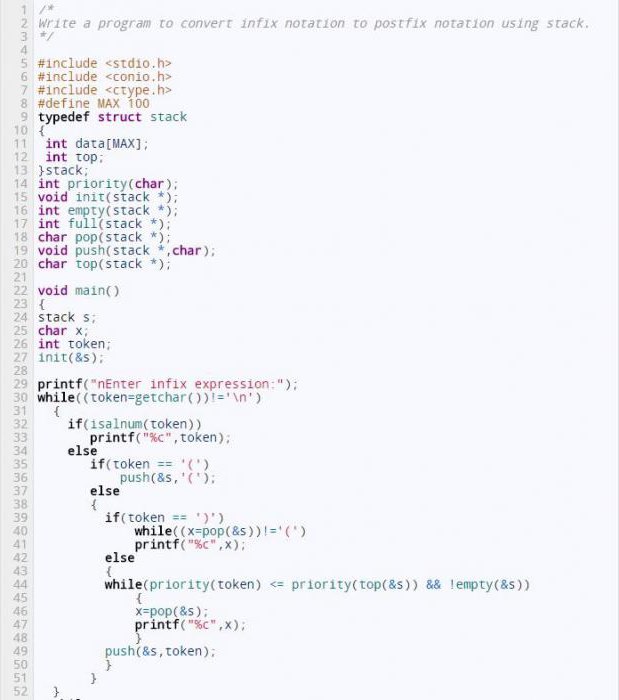
C-реализация обратной польской записи (приведен часть программы):
for (s = strtok(s, w); s; s = strtok(0, w)) <
#define rpnop(x) printf(«%с:», *s), b = pop(), a = pop(), push(x)
else if (*s == ‘+’) rpnop(a + b);
else if (*s == ‘-‘) rpnop(a — b);
else if (*s == ‘*’) rpnop(a * b);
else if (*s == ‘/’) rpnop(a / b);
Аппаратные реализации
В те времена, когда вычислительная техника стоила очень дорого, считалось хорошей идеей заставлять людей пользоваться ОПН. В 1960-х гг., как и сегодня, можно было купить калькуляторы, которые работают в обратной польской записи. Для сложения 2 и 3 в них необходимо ввести 2, затем 3 и нажать кнопку «плюс». На первый взгляд, ввод операндов до оператора казался сложным и трудно запоминающимся, но через некоторое время некоторые пристрастились к такому образу мышления и не могли понять, почему остальные настаивают на глупой инфиксной записи, которая так сложна и так ограничена.
Компания Burroughs даже построила мэйнфрейм, у которого не было никакой другой оперативной памяти, кроме стека. Единственное, что делала машина, – применяла алгоритмы и методы обратной польской записи к центральному стеку. Все ее операции расценивались как операторы ОПН, действие которых распространялось на n верхних значений. Например, команда Return брала адрес из вершины стека и т. д. Архитектура такой машины была простой, но недостаточно быстрой, чтобы конкурировать с более общими архитектурами. Многие, однако, до сих пор сожалеют о том, что такой простой и элегантный подход к вычислениям, где каждая программа была выражением ОПН, не нашел своего продолжения.
Одно время калькуляторы с обратной польской записью пользовались популярностью, и некоторые до сих пор отдают им предпочтение. Кроме того, были разработаны стек-ориентированные языки, такие как Forth. Сегодня он мало используется, но до сих пор вызывает ностальгию со стороны бывших его пользователей.
Так в чем смысл шутки об обратной польской сосиске?
Если считать сосиску оператором, то в инфиксной нотации она должна находиться внутри булки, как в обычном хот-доге. В обратной польской записи она находится правее двух половинок, готовая попасть между ними после вычисления. Теперь начинается самая трудная часть – горчица. Она уже находится на сосиске, т. е. уже вычислена как унарный оператор. Существует мнение, что горчица также должно быть показана как невычисленная и, следовательно, должна быть перемещена вправо от сосиски. Но возможно, для этого потребуется слишком большой стек.