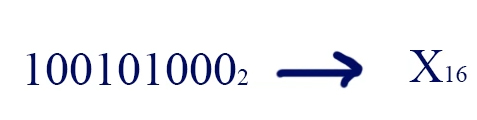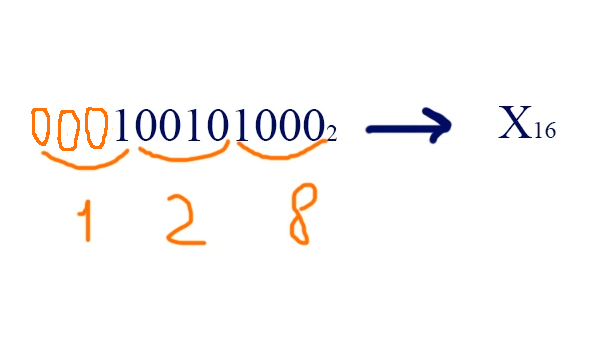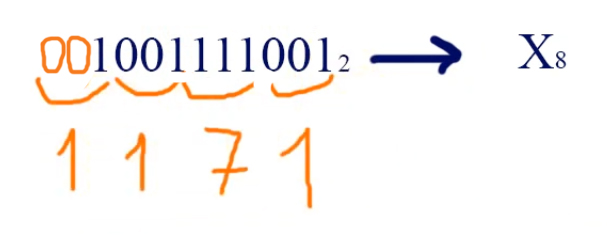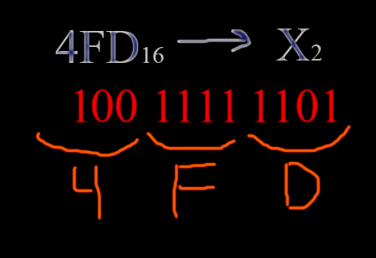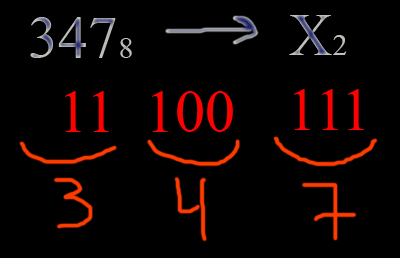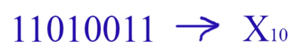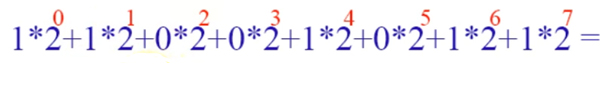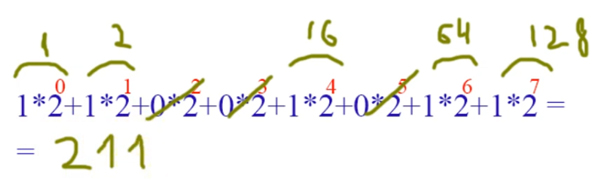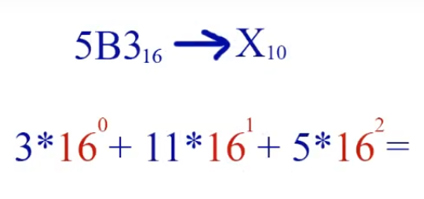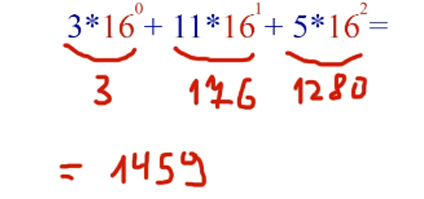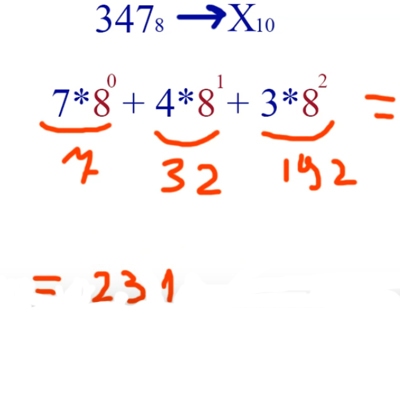Перевод в различные системы счисления теория

Системы счисления. Перевод чисел в различные системы счисления

Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления (CC).

СС — это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения, т.е. способ записи чисел.

По способу изображения чисел СС делятся на позиционные и непозиционные. Количество различных цифр, используемых для изображения числа в позиционной СС, называется основанием СС.Позиционная СС – арабская десятичная система, с основанием 10 (цифры от 0 до 9). Непозиционная СС – римская, в которой для каждого числа используется специфическое сочетание символов (семь знаков: I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000).

Двоичная ССимеет основание 2 и использует всего две цифры: 0 и 1. В 16-ой СС используется 16 различных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Перевод из недесятичной СС в десятичную.

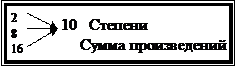
Внимание:цифра в записи числа – 1-ый множитель;

основание – 2-ой множитель;

позиция цифры – порядок степени второго множителя.

101110,101₍₂₎ = 1 * 2 5 + 0 * 2 4 + 1 * 2 3 + 1 * 2 2 + 1 * 2 1 + 0 * 2 0 + 1 * 2 -1 + 0 * 2 -2 + 1 * 2 -3 =

= 32 + 8 + 4 + 2 + 0,5 + 0,125 = 46,625₍₁₀₎ = 4 * 10 1 + 6 * 10 0 + 6 * 10 -1 + 2 * 10 -2 + 5 * 10 -3 .

Примечание: перевод целых чисел можно делать на калькуляторе.

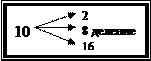
Перевод чисел из 10-ой СС в другую осуществляется с помощью
правила деления для целой части и правила умножения для дробной части.

Правило деления. Необходимо последовательно делить исходное число и получаемые частные на основание, выписывая остатки. Деление продолжается до тех пор, пока очередное частное не станет меньше основания. Затем нужно выписать последнее частное и за ним – полученные остатки в обратном порядке, заменив их цифрами соответствующей СС.

Правило умножения. Необходимо последовательно умножать исходную дробь и дробные части получаемых произведений на основание. Целые части произведений, замененные цифрами соответствующей СС, и дают искомый код. В общем случае перевод осуществляется приблизительно.

Перевод чисел из 2-ой СС в 16-ую (8-ую) СС и обратнопроизводится без пересчета простой подстановкой. Такое упрощение объясняется соотношением оснований: 16 = 2 4 ; 8 = 2 3 .

Каждая цифра в 16-ой (8-ой) записи числа заменяется четырьмя (тремя) двоичными, обозначающими то же число. Двоичное число разбивается на тетрады (триады), каждая заменяется соответствующей 16-ичной цифрой. Шестнадцатеричные коды используются для сокращенной записи двоичных кодов. Ранее и восьмеричные коды использовались.

Двоичная арифметика.

Таблица сложения одноразрядных двоичных чисел. 0+0=0

Источник

Системы счисления (Теория)

Сегодня разберём теоретический аспект работы с различными системами счисления. Основными системами счисления являются: двоичная, восьмеричная, десятичная (наша родная) и шестнадцатиричная.

Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.

Для начала нужно написать себе в черновик следующую таблицу:

Давайте рассмотрим данную таблицу. В первом столбце идут числа от 0 до 15 в нашей родной десятичной системе счисления. Во втором столбце идут числа так же от 0 до 15, но уже в двоичной системе, а в третьем тоже от 0 до 15 в шестнадцатиричной системе счисления.

Написать числа от 0 до 15 в нашей родной десятичной системе не у кого затруднений не вызовет.

Числа в двоичной же системе лучше всего написать по следующему правилу: в младшем разряде чередуем ноль и единицу, в следующем разряде чередование нулей и единиц происходит в два раза медленнее (два нуля, две единицы, два нуля и т.д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.

В шестнадцатиричной системе счисления помимо наших привычных символов от 0 до 9 придуманы символы A, B, С, D, E, F, и из этих 16 символов (от 0 до 15) составляется любое число, так же как в нашей системе составляется любое число из десяти цифр (от 0 до 9).Соответственно, чтобы посчитать от 0 до 15 — нужно перебрать все символы, которые имеются в шестнадцатиричной системе (от 0 до F).

Теперь рассмотрим, как с помощью данной таблицы переводить из двоичной системы в шестнадцатиричную. Переведём число 100101000 из двоичной системы в шестнадцатиричную.

Чтобы выполнить данную задачу, необходимо разбить наше двоичное число по 4 цифры начиная с правого края, и каждую 4-ку цифр нужно найти в нашей таблице: 1000 — это будет 8, 0010 — 2, 0001 -это 1. В старшем разряде у нас осталась одна единица, мы её дополнили 3-мя нулями.

Значит число 100101000₂ в двоичной системе счисления будет 128₁₆ в шестнадцатиричной.

Перевод чисел из двоичной системы в восьмеричную
систему счисления.

Из двоичной системы в восьмеричную систему X₂ -> X₈ переводим точно так же, только теперь из таблицы берём не по четыре цифры, а по три цифры.

Таким образом, число 1001111001₂ в двоичной системе будет равно 1171₈ в восьмеричной системе.

Перевод чисел из шестнадцатиричной системы в двоичную
систему счисления.

Делаем точно так же, как и при переводе чисел из двоичной в шестнадцатиричную, но в обратном порядке. По таблице смотрим: D — 1101, F — 1111, 4 — 0100. Получается число 010011111101. Слева нули мы отбрасываем 10011111101.

Перевод чисел из восьмеричной системы в двоичную
систему счисления.

Поступаем, как мы поступали ранее. Разбиваем каждую цифру восьмеричной системы по 3 цифры двоичной системы, используя таблицу, которая приведена в начале статьи. Нули слева откидываем.

Перевод чисел из двоичной системы в десятичную
систему счисления.

Берём цифры двоичного числа, начиная с младшего разряда (т.е. справа), и начинаем умножать на двойку в соответствующей степени. Степень начинается с нуля и с каждым разом увеличивается на 1. Все эти произведения суммируем.

После вычисления получаем число в десятичной системе:

Перевод чисел из десятичной системы в двоичную
систему счисления.

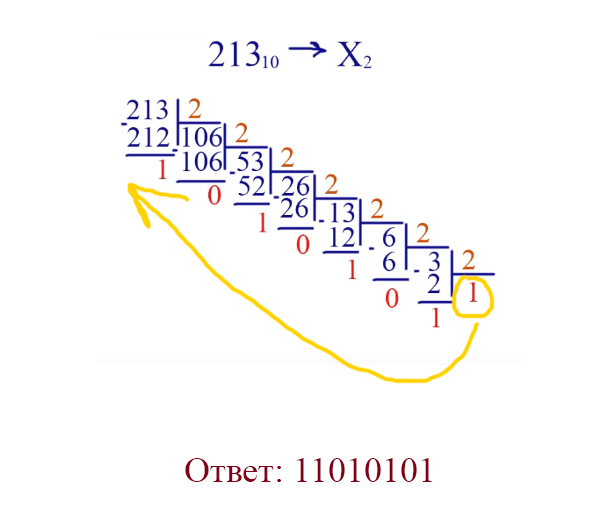
Рассмотрим, как перевести из десятичной системы в двоичную. Возьмём число 213.

Перевод чисел из шестнадцатиричной системы в восьмеричную систему
счисления и обратно.

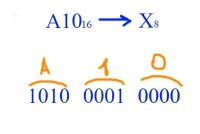
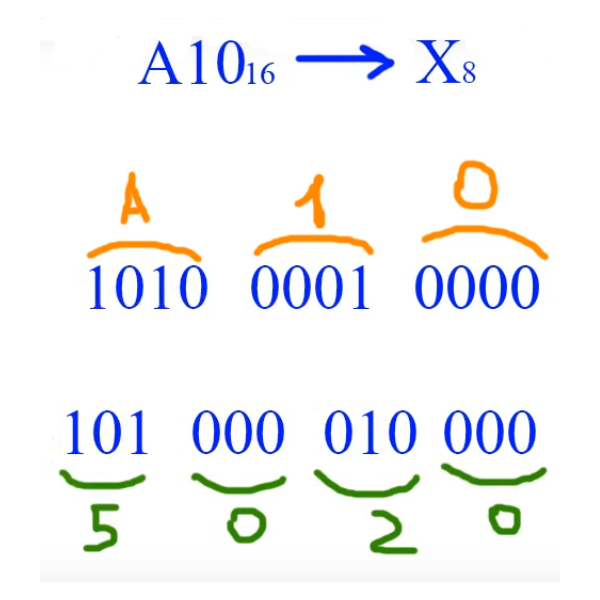
Переведём число A10 из шестнадцатиричной системы в восьмеричную A10₁₆ -> X₈.

Разбиваем каждую цифру шестнадцатиричного кода по 4-ри цифры двоичного кода из таблицы в начале статьи (Т.е. переводим число в двоичную систему). Полученное число разбиваем по три цифры — и собираем число уже в восьмеричной системе — как показано на рисунке. Обратно переводим аналогично, только в обратном порядке.

Перевод чисел из шестнадцатиричной системы в десятичную
систему счисления.

Переведём число 5B3 из шестнадцатиричной системы в десятичную систему счисления 5B3₁₆ -> X₁₀.

Действуем точно также, как при переводе из двоичной системы в десятичную, только умножаем цифры на 16 в соответствующей степени. Буквы превращаем в десятичные числа из таблицы. Начинаем, как всегда, справа, т.е. с младшего разряда.

Перевод чисел из десятичной системы в шестнадцатиричную
систему счисления.

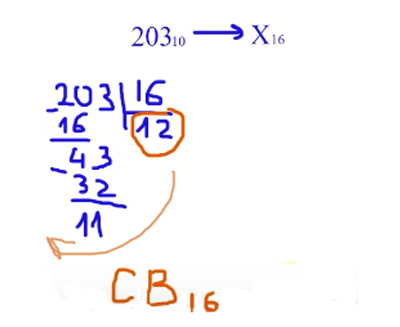
Переведём число 203 из десятичной системы в шестнадцатиричную систему счисления 203₁₀ -> X₁₆

Делим число на 16 до тех пор пока не получится число от 1 до 15. Записываем остатки в обратном порядке. Числа от 10 до 15 превращаем в буквы.

Перевод чисел из восьмеричной системы в десятичную
систему счисления.

Переведём число 347 из восьмеричной системы в десятичную систему счисления 347₈ -> X₁₀

Делаем аналогично предыдущим примерам, только теперь умножаем на 8 в соответствующей степени.

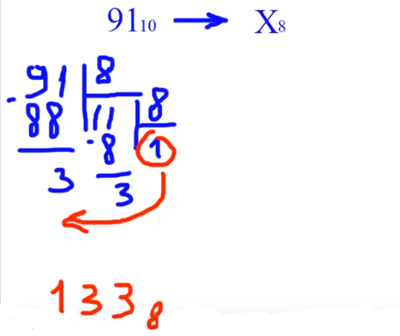
Перевод чисел из десятичной системы в восьмиричную
систему счисления.

Делаем аналогично предыдущим примерам.

Источник

Системы счисления

Страницы

Теория

• даёт представления множества чисел (целых или вещественных)

• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)

• отражает алгебраическую и арифметическую структуру чисел.

По современным данным, развитые системы нумерации впервые появились в древнем Египте. Для записи чисел египтяне применяли иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и операции сложения. Недостатки этой системы — невозможность записи больших чисел и громоздкость.

Классификация систем счисления

Позиционные системы счисления

Позиционные системы счисления (СС) — это системы счисления, в которых количественный эквивалент каждой цифры (её вес) зависит от ее положения (позиции) в записи числа.

Путем долгого развития человечество пришло к созданию позиционного принципа записи чисел, который состоит в том, что каждая цифра, содержащаяся в записи числа, занимает определенное место, называемое разрядом. Отсчет разрядов производится справа налево. Единица каждого следующего разряда всегда превосходит единицу предыдущего разряда в определенное число раз. Это отношение носит название основание системы счисления (у непозиционных систем счисления понятия «разряда» и «основания» отсутствуют).

Например:
число 237 состоит из 3 цифр. Понятно, что отдельно взятая цифра 7 больше чем цифра 2. Однако, в составе числа, двойка стоит на позиции сотен, а семёрка — на позиции единиц, поэтому количественное представление двойки — две сотни , или двести, а семёрка — всё та же семь.

Многие, кроме десятичной СС, о других позиционных системах не имеют представления, хотя и часто ими пользуются. Например:

1. шестидесятиричная (Древний Вавилон) — первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин);
2. двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 — «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава — всего 12;

В настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная.

Общее свойство всех позиционных систем счисления: при каждом переходе влево (вправо) в записи числа на один разряд величина цифры увеличивается (уменьшается) во столько раз, чему равно основание системы счисления.

Достоинства позиционных систем счисления:

• в позиционных системах счисления устранены все недостатки непозиционных:
• в них можно записать любое число (как натуральное, таки действительное);
• запись чисел компактна и удобна;
• благодаря поразрядной организации записи чисел с ними легко проводить математические операции.

Непозиционные системы счисления

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. Например: Римская система счисления.
Из многочисленных представителей этой группы в настоящее время сохранила свое значение лишь римская система счисления, где для обозначения цифр используются латинские буквы:

I	V	X	L	С	D	М
1	5	10	50	100	500	1000

С их помощью можно записывать натуральные числа. Например, число 1995 будет представлено, как MCMXCV (М-1000,СМ-900,ХС-90 и V-5).

Правила записи чисел в римской системе счисления:

• если большая цифра стоит перед меньшей, они складываются, например: VI – 6 (5+1);
• если меньшая цифра стоит перед большей, то из большей вычитается меньшая, причем в этом случае меньшая цифра уже повторяться не может, например: XL — 40 (50-10), XXL – нельзя;
• цифры М, С, Х, I могут повторяться в записи числа не более трех раз подряд;
• цифры D, L, V могут использоваться в записи числа только по одному разу.

Например, запись XXX обозначает число 30, состоящее из трех цифр X, каждая из которых, независимо от места ее положения в записи числа, равна 10. Запись MCXX1V обозначает 1124, а самое большое число, которое можно записать в этой системе счисления, это число MMMCMXCIX (3999). Для записи еще больших чисел пришлось бы вводить все новые обозначения. По этой причине, а также по причине отсутствия цифры ноль, римская система счисления не годится для записи действительных чисел.
Таким образом, можно констатировать следующие основные недостатки непозиционных систем счисления:

• в них нельзя записать любое число;
• запись чисел обычно громоздка и неудобна;
• математические операции над ними крайне затруднены.

Алфавит и основание системы счисления

Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.

Развёрнутая форма представления числа

Системы счисления, используемые в вычислительной технике

Несмотря на то, что исторически человек привык работать в десятичной системе счисления, с технической точки зрения она крайне неудобна, так как в электрических цепях компьютера требовалось бы иметь одновременно десять различных сигналов. Тем не менее, такие схемы существуют в некоторых видах микрокалькуляторов.

Чем меньше различных сигналов в электрических цепях, тем проще микросхемы, являющиеся основой конструкции большинства узлов ЭВМ, и тем надежнее они работают.

Наименьшее основание, которое может быть у позиционных систем счисления это – двойка. Именно поэтому двоичная система счисления используется в вычислительной технике, а двоичные наборы приняты за средство кодирования информации. В компьютере имеются только два устойчивых состояния работы микросхем, связанных с прохождением электрического тока через данное устройство (1) или его отсутствием (0). Говоря точнее, (1) кодирует высокое напряжение в схеме компьютера, а (0) – низкое напряжение.

Если вспомнить, что двоичная система счисления обладает самыми маленькими размерами таблиц сложения и умножения, то можно догадаться, что этот факт должен сильно радовать конструкторов ЭВМ, поскольку обработка сигнала в этом случае будет также самой простой. Таким образом, двоичная система счисления, с точки зрения организации работы ЭВМ, является наилучшей.

Мы уже говорили о преимуществах двоичной системы счисления с технической точки зрения организации работы компьютера. Зачем нужны другие системы счисления, кроме, естественно, еще и десятичной, в которой человек привык работать? Чтобы ответить на него, возьмем любое число в десятичной системе счисления, например 255, и переведем его в другие системы счисления с основаниями, кратными двойке:

Чем меньше основание системы счисления, тем больше разрядов требуется для его записи то есть, тем самым мы проигрываем в компактности записи чисел и их наглядности. Поэтому, наряду с двоичной и десятичной системами счисления, в вычислительной технике применяют так же запись чисел в 8-и 16-ричных системах счисления. Поскольку их основания кратны двойке, они органично связаны с двоичной системой счисления и преобразуются в эту систему наиболее быстро и просто (по сути они являются компактными видами записи двоичных чисел). Все другие системы счисления представляют для вычислительной техники чисто теоретический интерес.

Источник