Как правильно преобразовывать в сферические координаты?
Всем здравствуйте, возник вопрос по переводу декартовых координат в сферические и обратно. Просмотрел формулы на википедии, поспрашивал в чате.
Сделал конвертер:
Проверил что работают взяв координаты точки и прогнав туда-обратно через обе функции получил ту же самую точку,
но сферические координаты задаются не по ISO (фи[0 до 360] тета [-90 до 90]), а в другом представлении (фи83 тета [-180 до 180]).
Перевод нужен именно пользователю, который задаёт сферические координаты, и для просчёта длин отрезков/площадей.
Подскажите пожалуйста как исправить код к таким координатам.
сферические координаты задаются не по ISO (фи[0 до 360] тета [-90 до 90]), а в другом представлении (фи160 тета [-180 до 180]).
Точно не перепутаны местами углы? Так-то диапазон для одно из них (долгота) должен быть 360, для другого (широта) 180.
Если же поменять местами, то есть в одном случае долгота от 0 до 360 и широта от -90 до 90, а в другом долгота от -180 до 180 и широта от 0 до 180, то необходимо добавить преобразование
где (phi,theta) в ISO, а (phi1,theta1) в формате пользователя. Обратное преобразование выписывается аналогично:
Скажем, нужно Вам, чтобы SphericalToCartesian интерпретировала входные phi,theta в пользовательском формате. Вы пишите
Аналогично для другого преобразования.
Сразу прошу извинить, что не указал что тут используються радианы, а не градусы.
Попробовал ваш способ, не удалось получить необходимые градусы и радианы.
для ясности предоставлю схематичный рисунок: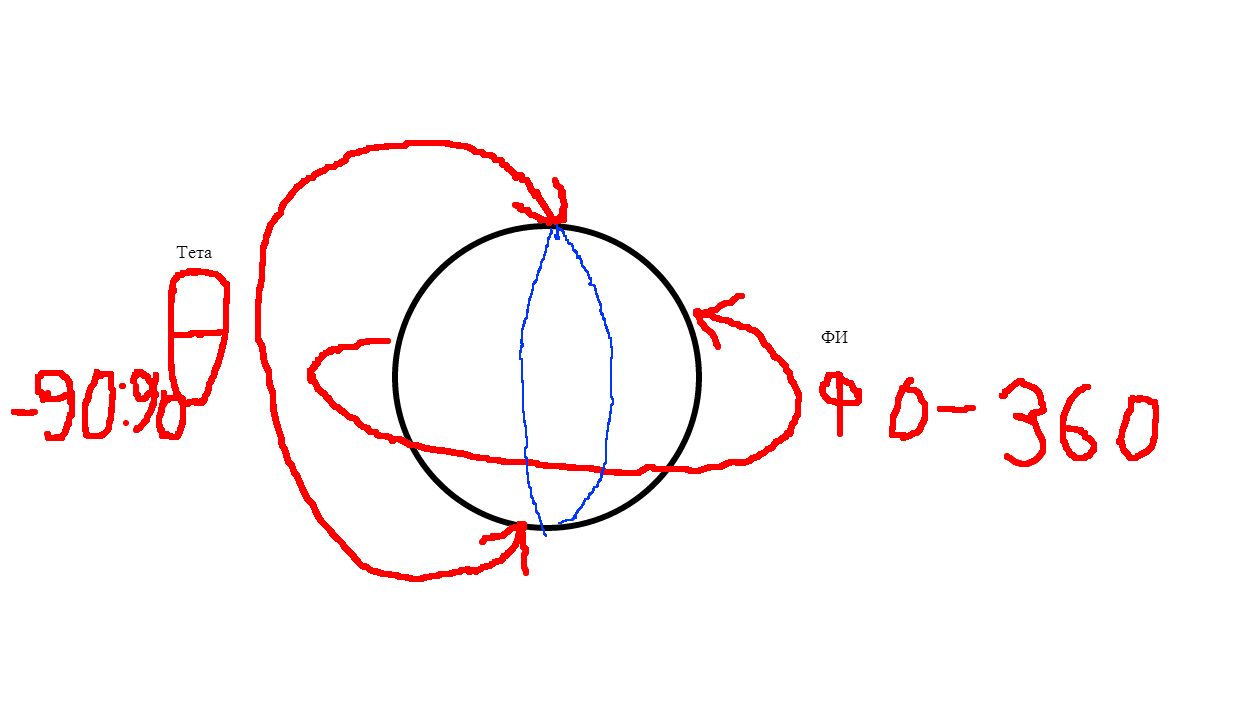
И ссылку на сам проект.
В методе Start() скрипта Camera устанавливаеться точка, но с вашими правками, вершина этой сферы по указанным координатам оказалась на экваторе.
TestConverter — новый конвертер
Converter — конвертер с кодом из поста
Не сочтите за наглость, просто очень долго с этим вопросом мучаюсь, не могли бы вы исправить мой косяк с конвертацией, так чтобы градусы образовывались как на рисунке выше.
Вопрос по строчке, Asin — арксинус принимает только один аргумент, что нужно туда подставить?
youngmysteriouslight, посмотрел на ваши формулы, не получилось получить нужные, но благодаря им смог исправить свои.
Справедливо только для Unity — так как оси в ней перевёрнуты.
Проверил что код работает тестом установки точки на сферу, получив после прямой и обратной конвертации туже самую точку:
Сферические координаты (сферическая система координат)
Для введения сферической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом ( начало сферической системы координат ) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).
В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки — ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки — это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .
Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).
Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат ( связанную с данной прямоугольной ).
Переход от сферических координат к декартовым (прямоугольным)
Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем
Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам
Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).
Пример 2.13. В сферической системе координат :
а) построить координатные поверхности ;
б) найти сферические координаты точки , если известны её прямоугольные координаты ;
в) найти прямоугольные координаты точки , если известны её сферические координаты: .
Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина — с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .
б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем
Документация
Сферические координаты
Поддержка сферических координат
Сферические координаты описывают вектор или точку на пробеле с расстоянием и двумя углами. Расстояние, R, является обычной Евклидовой нормой. Существует несколько соглашений относительно спецификации этих двух углов. Они включают:
Азимут и углы вертикального изменения
Программное обеспечение Phased Array System Toolbox™ исходно поддерживает представление азимута/вертикального изменения. Программное обеспечение также обеспечивает функции для преобразования между представлением азимута/вертикального изменения и другими представлениями. См. Углы Phi и Теты и U и V Координат.
Азимут и углы вертикального изменения
В программном обеспечении Phased Array System Toolbox преобладающее соглашение для сферических координат следующие:
Используйте угол азимута, az, и угол вертикального изменения, el, чтобы задать местоположение точки на сфере единичного радиуса.
Задайте все углы в градусах.
Перечислите координаты в последовательности ( az, el, R).
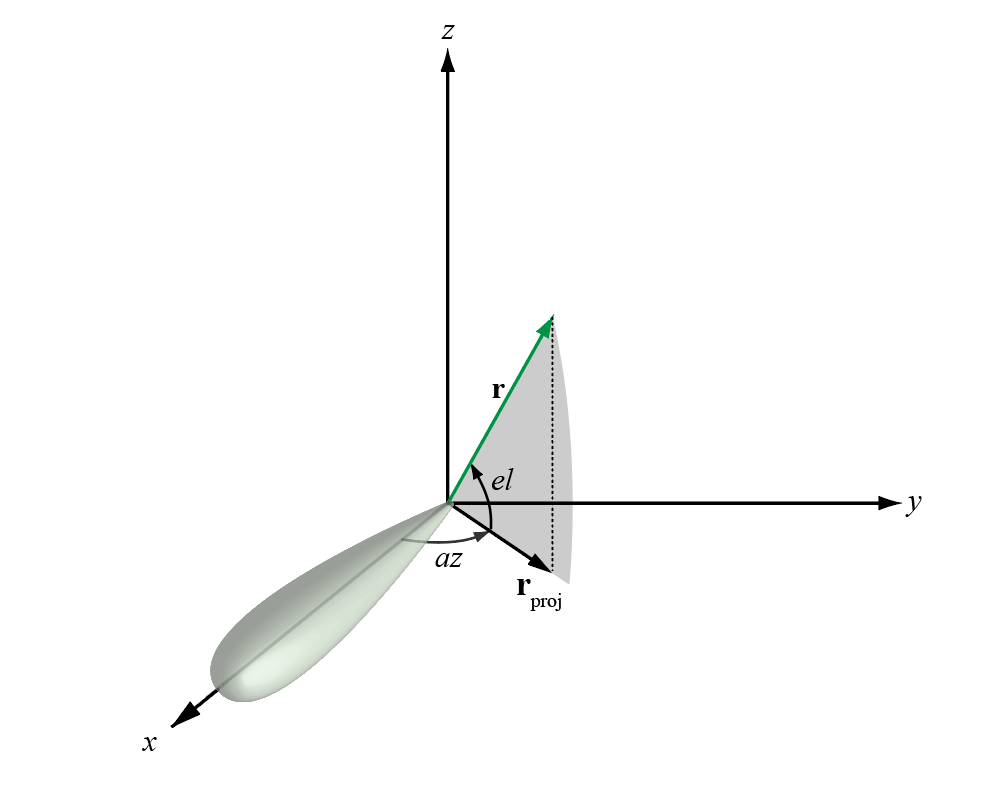
azimuth angle вектора является углом между x — ось и ортогональной проекцией вектора на плоскость xy. Угол положителен в движении от оси x к оси y. Углы азимута находятся между –180 и 180 градусами. elevation angle является углом между вектором и его ортогональной проекцией на xy — плоскость. Угол положителен при движении к положительному z — ось от плоскости xy. По умолчанию направление опорного направления элемента или массива выравнивается с положительным x — ось. Направление опорного направления является направлением основного лепестка элемента или массива.
Примечание
Угол вертикального изменения иногда задается в литературе как угол, который вектор делает с положительным z — ось. MATLAB ® и продукты Phased Array System Toolbox не используют это определение.
Этот рисунок иллюстрирует угол азимута и угол вертикального изменения для вектора, показавшего зеленой сплошной линией.
Phi и Theta Angles
Как альтернатива азимуту и углам вертикального изменения, можно использовать углы, обозначенные φ и θ, чтобы выразить местоположение точки на сфере единичного радиуса. Чтобы преобразовать представление φ/θ и от соответствующего представления азимута/вертикального изменения, используйте координатные функции преобразования, phitheta2azel и azel2phitheta .
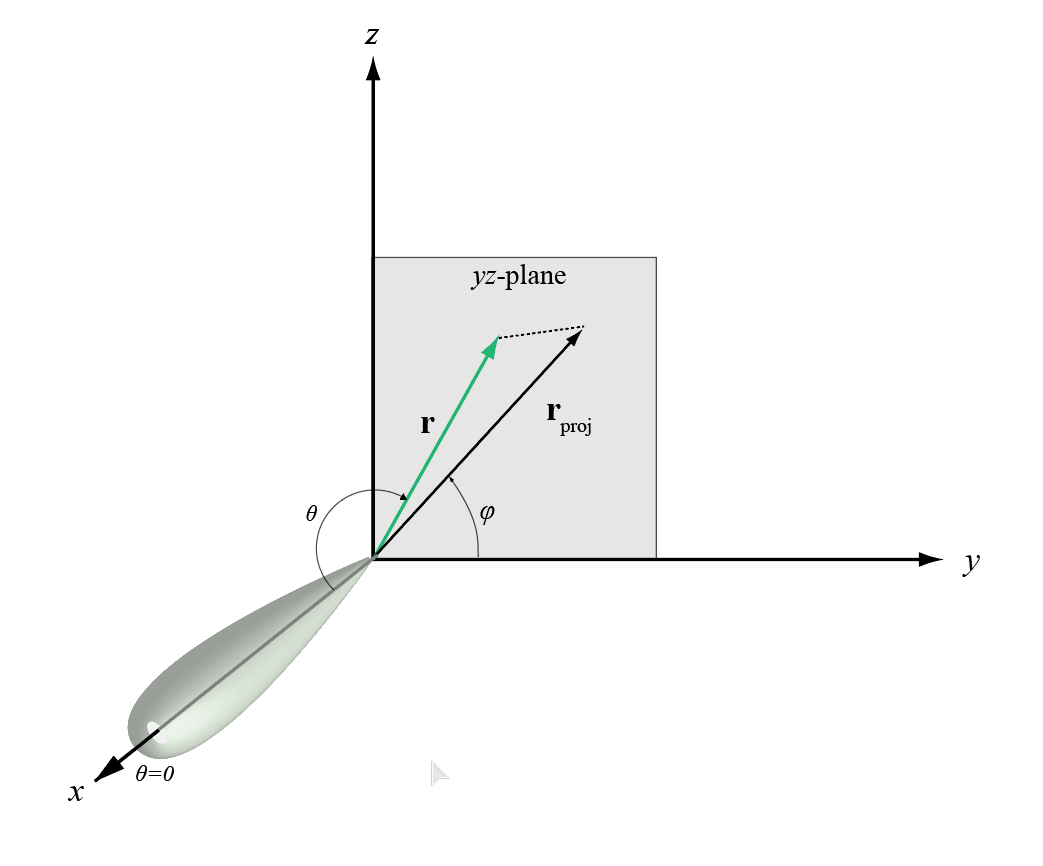
phi угол ( φ) является углом от положительного y — ось к ортогональной проекции вектора на плоскость yz. Угол положителен к положительному z — ось. phi угол между 0 и 360 градусами. Угол теты ( θ) является углом от x — ось к самому вектору. Угол положителен к плоскости yz. Угол теты между 0 и 180 градусами.
Фигура иллюстрирует phi и тету для вектора, который появляется как зеленая сплошная линия.
Координатные преобразования между φ/θ и az/el описаны следующими уравнениями
sin e l = sin ϕ sin θ tan a z = cos ϕ tan θ cos θ = cos e l cos a z tan ϕ = tan e l / sin a z
U и V координат
В радарных приложениях часто полезно параметрировать полушарие x ≥ 0 координат использования, обозначенных u и v.
Чтобы преобразовать φ/θ представление и от соответствующего u/ v представление, используйте координатные функции преобразования phitheta2uv и uv2phitheta .
Чтобы преобразовать представление азимута/вертикального изменения и от соответствующего u/ v представление, используйте координатные функции преобразования azel2uv и uv2azel .
Можно задать u и v в терминах φ и θ:
u = sin θ cos ϕ v = sin θ sin ϕ
В этих выражениях φ и θ являются phi и углами теты, соответственно.
В терминах азимута и вертикального изменения, u и координаты v
u = cos e l sin a z v = sin e l
Значения u и v удовлетворяют неравенствам
− 1 ≤ u ≤ 1 − 1 ≤ v ≤ 1 u 2 + v 2 ≤ 1
С другой стороны phi и углы теты могут быть записаны в терминах использования v и u
tan ϕ = u / v sin θ = u 2 + v 2
Азимут и углы вертикального изменения могут также быть записаны в терминах u и v
sin e l = v tan a z = u 1 − u 2 − v 2
Преобразование между прямоугольными и сферическими координатами
Следующие уравнения задают отношения между прямоугольными координатами и ( az, el, R) представление, используемое в программном обеспечении Phased Array System Toolbox.
Преобразовывать прямоугольные координаты в ( az, el, R):
R = x 2 + y 2 + z 2 a z = tan − 1 ( y / x ) e l = tan − 1 ( z / x 2 + y 2 )
Преобразовывать ( az, el, R) к прямоугольным координатам:
x = R cos ( e l ) cos ( a z ) y = R cos ( e l ) sin ( a z ) z = R sin ( e l )
При определении местоположения цели относительно поэтапного массива распространено относиться к своему расстоянию и направлению от массива. Расстояние от массива соответствует R в сферических координатах. Направление соответствует углы вертикального изменения и азимут.
Совет
Преобразовывать между прямоугольными координатами и ( az, el, R), используют функции MATLAB cart2sph и sph2cart . Эти функции задают углы в радианах. Чтобы преобразовать между степенями и радианами, использовать deg2rad и rad2deg .
Поперечные углы
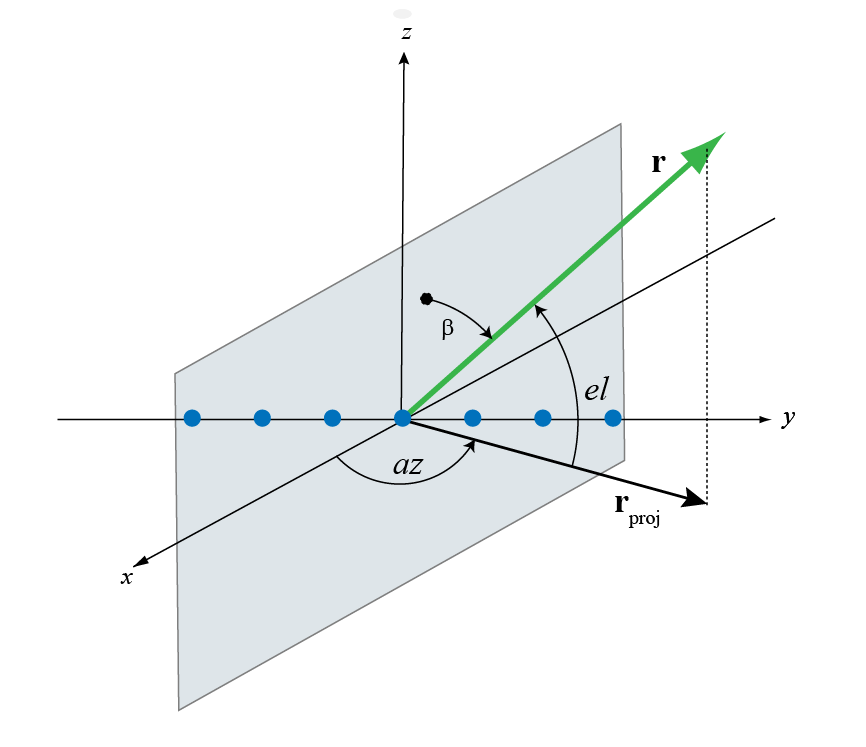
Broadside angles полезен при описании ответа универсальной линейной матрицы (ULA). Ответ массивов зависит непосредственно от поперечного угла а не от углов вертикального изменения и азимута. Начните с ULA и чертите плоскость, ортогональную к оси ULA как показано синего цвета в фигуре. Поперечный угол, β, является углом между плоскостью и направлением сигнала. Чтобы вычислить поперечный угол, создайте линию из любой точки на пути прохождения сигнала к плоскости, ортогональной к плоскости. Угол между этими двумя линиями является поперечным углом и находится в интервале [–90 °, 90 °]. Поперечный угол положителен, когда измерено к положительному направлению оси массивов. Нулевые степени указывают на путь прохождения сигнала, ортогональный к оси массивов. ±90 ° указывают на пути вдоль оси массивов. Все пути прохождения сигнала, имеющие тот же поперечный угол, формируют конус вокруг оси ULA.
Преобразование из угла азимута, az, и угла вертикального изменения, el, к поперечному углу, β,
β = sin − 1 ( sin ( a z ) cos ( e l ) )
Это уравнение показывает это
Для угла вертикального изменения нуля поперечный угол равняется углу азимута.
Углы вертикального изменения одинаково выше и ниже результата плоскости xy в идентичных поперечных углах.
Можно преобразовать от поперечного угла до угла азимута, но необходимо задать угол вертикального изменения
a z = sin − 1 ( sin β cos ( e l ) )
Поскольку пути к сигналам для данного поперечного угла, β, формируют конус вокруг оси массивов, вы не можете задать угол вертикального изменения произвольно. Угол вертикального изменения и поперечный угол должны удовлетворить
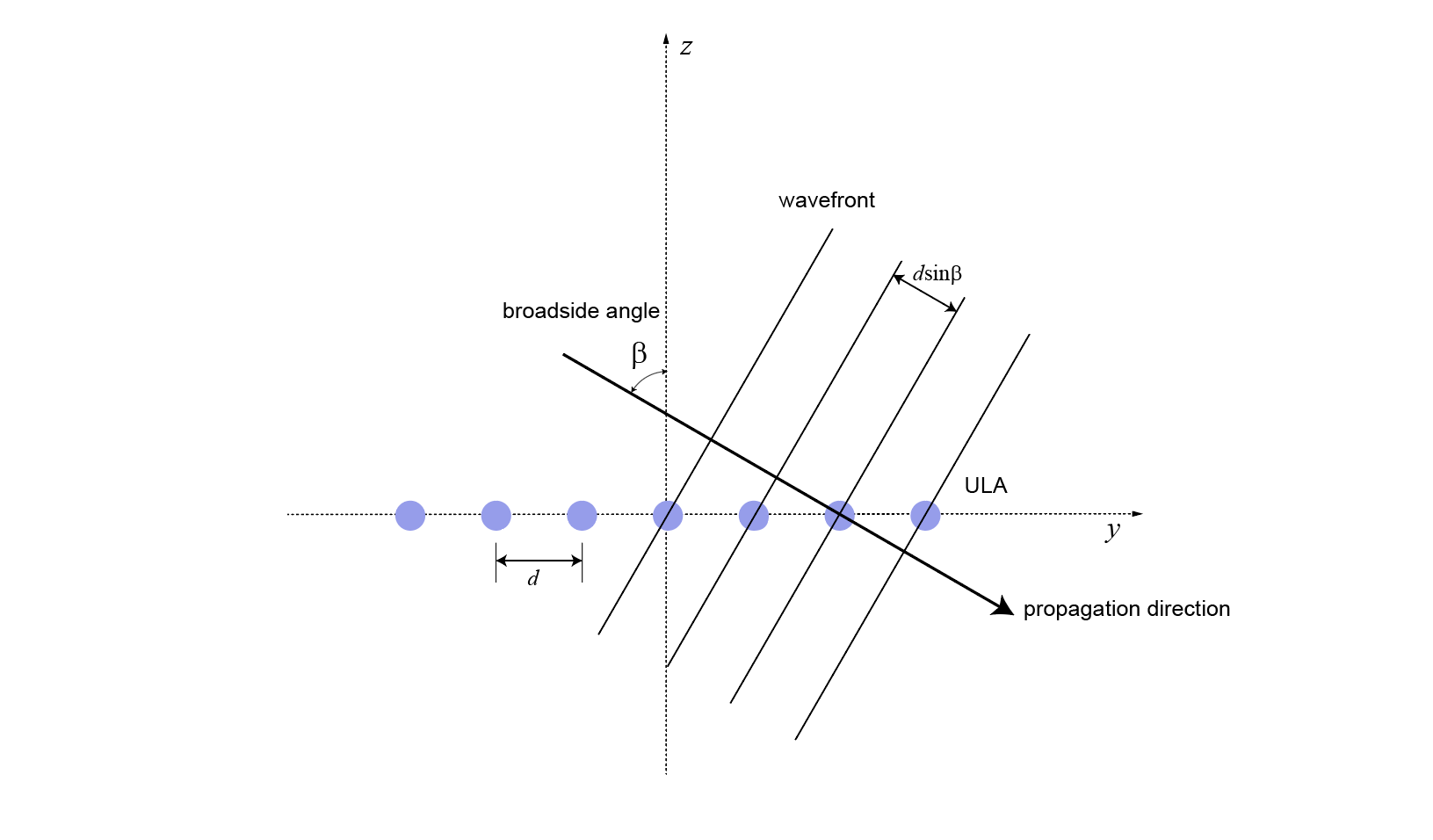
Следующая фигура изображает ULA с распределенными метрами d элементов независимо вдоль y — ось. ULA облучается плоской волной, испускаемой из точечного источника в далеком поле. Для удобства угол вертикального изменения является нулевыми степенями. В этом случае направление сигнала находится в xy — плоскость. Затем поперечный угол уменьшает до угла азимута.
Из-за угла прибытия элементы массива одновременно не освещаются плоской волной. Дополнительное расстояние инцидентными перемещениями волны между элементами массива является d sinβ , где d является расстоянием между элементами массива. Постоянная задержка, τ, между элементами массива
где c является скоростью волны.
Для поперечных углов ±90 ° сигнал является инцидентом на массиве, параллельном оси массивов, и задержка между датчиками равняется ±d/c. Для поперечного угла нуля плоская волна освещает все элементы ULA одновременно, и задержка между элементами является нулем.
Программное обеспечение Phased Array System Toolbox обеспечивает функции az2broadside и broadside2az для преобразования между азимутом и поперечными углами.
Преобразуйте между поперечными углами и азимутом и вертикальным изменением
Следующие примеры показывают, как использовать az2broadside и broadside2az функции.
Цель расположена под углом азимута 45 ° и под углом вертикального изменения 60 ° относительно ULA. Определите соответствующий поперечный угол.
Вычислите азимут для инцидентного сигнала, прибывающего в поперечный угол 45 ° и вертикальное изменение 20 °.