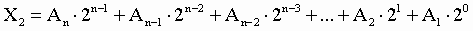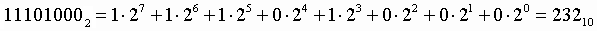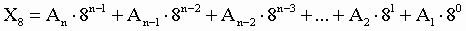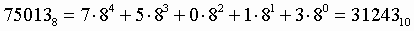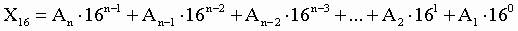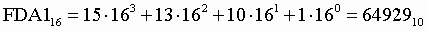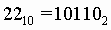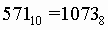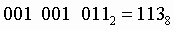Перевод в шестнадцатеричную систему счисления алгоритм - Uchenik.top

Содержание

Перевод чисел в шестнадцатеричную систему счисления

Решение получаем через калькулятор. Переводим целую часть числа ( 56 ).

Целая часть от деления	Остаток от деления
56 div 16 = 3	56 mod 16 = 8 (56 — 3 *16)
3 div 16 = 0	3 mod 16 = 3
0 div 16 = 0	0 mod 16 = 0

Остаток от деления записываем в обратном порядке. Получаем число в 16-ой системе счисления: 038
56 = 038₁₆

Для перевода дробной части числа последовательно умножаем дробную часть на основание 16. В результате каждый раз записываем целую часть произведения.
0.567*16 = 9.072 (целая часть 9 )
0.072*16 = 1.152 (целая часть 1 )
0.152*16 = 2.432 (целая часть 2 )
0.432*16 = 6.912 (целая часть 6 )
Получаем число в 16-ой системе счисления: 9126
0.567 = 9126₁₆

Таким образом, число 56,567 в шестнадцатеричной системе счисления записывается как 38,9126.

Пример 2 . Перевести число 0101110,011 в шестнадцатеричное представление.
Переводим целую часть числа. Для этого разделим исходный код на группы по 4 разряда.
0101110₂ = 0010 1110 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Шестнадцатеричная СС
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Получаем число: 0010 1110 ₂ = 2E₁₆

Переводим дробную часть числа. Для этого разделим исходный код на группы по 4 разряда.
011₂ = 0110₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 0110₂ = 6₁₆

Пример 3 . Перевести число 456,54₈ в шестнадцатеричное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 456₈ = 100101110₂

Переводим дробную часть числа.
Получаем число: 54₈ = 101100₂
Переводим целую часть числа. Для этого разделим исходный код на группы по 4 разряда.
100101110₂ = 0001 0010 1110 ₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 0001 0010 1110 ₂ = 12E₁₆

Переводим дробную часть числа. Для этого разделим исходный код на группы по 4 разряда.
101100₂ = 1011 0000₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 1011 0000₂ = B0₁₆

Источник

Алгоритм перевода чисел из одной системы счисления в другую

1. Из десятичной системы счисления:

o разделить число на основание переводимой системы счисления;

o найти остаток от деления целой части числа;

o записать все остатки от деления в обратном порядке;

2. Из двоичной системы счисления

o Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;

o Для перевода числа в восьмеричную необходимо разбить число на триады.
Например, 1000110 = 1 000 110 = 106₈

o Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 46₁₆

Таблицы для перевода:

Двоичная СС	Шестнадцатеричная СС
A
B
C
D
E
F

Двоичная СС

Восьмеричная СС

Рассмотрим основные правила перевода.

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:

Таблица 4. Степени числа 2

n (степень)

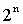Пример .Число 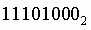перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:

Таблица 5. Степени числа 8

n (степень)

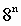Пример .Число 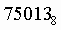перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:

Таблица 6. Степени числа 16

n (степень)

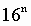Пример .Число 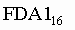перевести в десятичную систему счисления.

Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример.Число 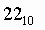перевести в двоичную систему счисления.

Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

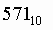
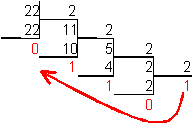
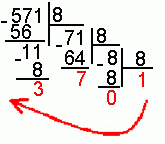
Пример.Число перевести в восьмеричную систему счисления.

Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

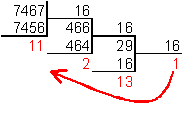
Пример.Число перевести в шестнадцатеричную систему счисления.

Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример.Число перевести в восьмеричную систему счисления.

Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример.Число 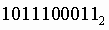перевести в шестнадцатеричную систему счисления.

Источник

Переведем числа из десятичной системы счисления в шестнадцатеричную систему счисления.

Алгоритм перевода целых чисел из десятичной в шестнадцатеричную систему счисления: Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

а)Число 22₍₁₀₎ перевести в шестнадцатеричную систему счисления.

б) Число перевести 35,5625 ₍₁₀₎ в шестнадцатеричную систему счисления.

Перевод целой части	Перевод дробной части

Задание 2. Перевести данное число в десятичную систему счисления:

Алгоритм перевода чисел из двоичной системы счисления в десятичную систему счисления: Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики

100101101,1₍₂₎=1×2 8 +0×2 7 +0×2 6 +1×2 5 +0×2 4 +1×2 3 +1×2 2 +0×2 1 +1×2 0 +1×2 -1 = =256+32+8+4+1+0,5 =301, 5₍₁₀₎

Алгоритм перевода чисел из восьмеричной системы счисления в десятичную систему счисления. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

1056,4₍₈₎=1×8 3 +0×8 2 +5×8 1 +6×8 0 +4×8 -1 =512+40+6+0, 5=550, 5₍₁₀₎

Алгоритм перевода чисел из шестнадцатиричной системы счисления в десятичную систему счисления. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики

385,64₍₁₆₎=3×16 2 +8×16 1 +5×16 0 +6×16 -1 +4×16 -2 = 768+128+5+0,375+0,015625 =901,390625 ₍₁₀₎

Задание 3 Сложите числа:

а) сложение двузначных чисел, действия выполняем по правилам двоичной арифметики:

+	101101110,10
1100100,11
111010011,01

Проверка: правильность вычислений проверим переводом исходных данных и результатов в десятичную систему счисления

101101110,1 ₍₂₎ =1×2 8 +0×2 7 +1×2 6 +1×2 5 +0×2 4 +1×2 3 +1×2 2 +1×2 1 +0×2 0 +1×2 -1 = 256+64+ +32+8+4+2+0,5 =366, 5₍₁₀₎

1100100,11 ₍₂₎ =1×2 6 +1×2 5 +0×2 4 +0×2 3 +1×2 2 +0×2 1 +0×2 0 +1×2 -1 +1×2 -2 = 64+ 32+4+0,5+0,25=100,75₍₁₀₎

111010011,01 ₍₂₎= 1×2 8 +1×2 7 +1×2 6 +0×2 5 +1×2 4 +0×2 3 +0×2 2 +1×2 1 +1×2 0 +0×2 -1 +1×2 -2 = 256+128+64+ 16+2+1+0,25 =467, 25₍₁₀₎

б) сложение восьмеричных чисел действия выполняем по правилам восьмеричной арифметики, (см. приложении А таблицу 1).

+	3015,10
527,34
3544,44

3015,1₍₈₎ =3×8 3 +0×8 2 +1×8 1 +5×8 0 +1×8 -1 =1536+8+5+0, 5=1549, 125₍₁₀₎

527,34₍₈₎ =5×8 2 +2×8 1 +7×8 0 +3×8 -1 +4×8 -2 =320+16+7+0, 375+0,0625=343, 4375₍₁₀₎

3544,44₍₈₎ =3×8 3 +5×8 2 +4×8 1 +4×8 0 +4×8 -1 +4×8 -2 =1536+320+4+0,5+0,0625= =1892,5625 ₍₁₀₎

Задание 4 Выполните вычитание.

а) вычитание двузначных чисел, действия выполняем по правилам двоичной арифметики

б) вычитание восьмеричных чисел действия выполняем по правилам восьмеричной арифметики

724,50

65,14

37,44

Задание 4 Выполните вычитание.

а) вычитание двузначных чисел, действия выполняем по правилам двоичной арифметики

б) вычитание восьмеричных чисел действия выполняем по правилам восьмеричной арифметики

724,50

65,14

37,44

Задание 5. Выполните умножение.

а) Умножение двузначных чисел, действия выполняем по правилам двоичной арифметики

б) Умножение восьмеричных чисел действия выполняем по правилам восьмеричной арифметики (см. приложении А таблицу 2).

´	47,2
64,14
+ + +
4000,270

Задание 6. Составить таблицу. Высказывания расчлените на простые и запишите символически, введя буквенные обозначения для простых их составляющих. Определите значения истинности высказываний:

«Если 12 делится на 6, то 12 делится на 3».

Введем обозначение для простых высказываний:

Тогда высказывание «Если 12 делится на 6, то 12 делится на 3», можно записать символически A®B.

Т.е. высказывание-посылка «12 делится на 6» истинно и высказывание-следствие «12 делится на 3» истинно, то и составное высказывание по определению импликации истинно.

Ответ:Высказывание«Если 12 делится на 6, то 12 делится на 3», истинно.

Задание 6. Составить таблицу истинности для следующих формул и укажите, какие из этих формул являются выполнимыми, какие – опровержимыми, какие – тождественно истинными (тавтологиями), какие – тождественно ложными (противоречиями):ØAÙ( BÚC )

Составить таблицу истинности для логического выражения:

Переменные	Промежуточные логические формулы	Формула
A	B	C

Ответ:Формула в некоторых случаях принимает значения 1, а в некоторых -0, то есть является выполнимой.

1. Информатика базовый курс: учебное пособие/под ред. С.В Симоновича.-2-е изд.- Спб.: Питер, 2007.-640 с.

2. Фатеева Н.М. Арифметические и логические основы компьютера: учебно-методические указания / Н.М. Фатеева, О.А. Возилкина, Н.В. Тумбаева. Барнаул: Изд-во АГАУ, 2008. 53 с.

Таблица 1 Cложение восьмеричных чисел

Таблица 2 Умножения восьмеричных чисел:

ПРИЛОЖЕНИЕ В
Пример оформления титульного листа