Способы выражения количественного
Состава растворов
Количественный состав раствора определяется концентрацией, т.е. относительным содержанием каждого из компонентов, составляющих раствор.
Растворы с большой концентрацией вещества называются концентрированными, с малой — разбавленными.
Известно много способов выражения концентрации, основанных на постоянстве количества раствора, растворенного вещества, растворителя или объема раствора.
При постоянном количестве раствора концентрации выражаются в процентах и в долях.
Весовые проценты. Концентрация выражается числом весовых частей растворенного вещества в 100 весовых частях раствора. Например, 10 % раствор NaCl — это смесь 10 г NaCl и 90 г H2O.
Молекулярные проценты. Концентрация выражается числом грамм — молекул (молей) растворенного вещества M в 100 — M молях растворителя.
Концентрация 40 % — ного раствора H2SO4 в молях % вычисляется следующим образом:
100 ∙ 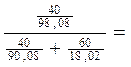
100 — 10,91 = 89,09 моль % H2O
Атомные проценты. Определяется числом n — атомов растворенного компонента m, приходящихся на 100 — m грамма растворителя.
Для сплава, содержащего 66,7 % Na и 33,3 % К состав компонентов в весе % вычисляется следующим образом:

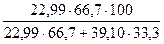
100 – 54,08 = 45,92 веса % К
здесь 22,99 и 39,10 – атомные веса соответственно Na и К.
Весовая доля, мольная доля, атомная доля составляет соответственно одну сотую от весовых, молекулярных и атомных процентов.
При постоянном количестве растворителя концентрация выражается моляльностью и числом граммов растворенного вещества на 1 кг растворителя.
Моляльность.Концентрация определяется числом молей (m) растворенного вещества в 1 кг растворителя.
При постоянном объеме раствора концентрация выражается через молярность, нормальность и титральность.
Молярность. Концентрация определяется числом молей растворенного вещества (M), содержащихся в 1 л. раствора. Так, одномолярный раствор обозначается 1 М и т.д. Например, 2 M раствор H2SO4, значит в л раствора содержится 2 г — моль H2SO4 или 2 ∙ 98 = 196 г H2SO4
Нормальность. Концентрация определяется числом 2 эквивалентов растворенного вещества, содержащихся в 1 л раствора. Так 2 н H2SO4 , значит, что в 1 л раствора содержится 2 г — эквивалента H2SO4. 1 г – эквивалент H2SO4 равен 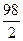
Титральность. Концентрация определяется количеством грамма вещества, содержащегося в 1 см 3 раствора (1 мл.)
Дата добавления: 2016-12-09 ; просмотров: 3322 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Определение атомных и весовых количеств элементов. Перевод атомных количеств в весовые проценты. Расчет средних содержаний
Лабораторная работа № 1
Задание:
Даны количественные содержания основных окислов по результатам силикатного анализа. Требуется пересчитать весовые проценты окислов SiO2, Al2O3, Fe2O3, FeO, TiO2, MnO, MgO, CaO, Na2O, K2O, P2O5, SO3 на весовые проценты элементов, с составлением таблицы используя нижеприведенный порядок расчетов. Найти дисперсию и стандартное отклонение по каждому элементу.
Ход работы:
1. Взять данные по атомному весу элементов О (16), Si(28), Al (27), Fe (55,85), Ti (48), Mn (55), Mg (24), Ca (40), Na (23), K (39), P (31).
2. Рассчитать молекулярный вес каждого окисла.
3. По соотношениям молекулярного веса окисла и его атомного веса, молекулярного веса окисла и его содержания в весовых процентах рассчитываем концентрацию элемента в весовых процентах, исходя из пропорции:
— cодержание элемента в вес.%– атомный вес элемента;
— cодержание окисла в вес.% – молек.вес окисла
Пример расчета для оксида кремния SiO2.
Атомный вес О=16; атомный вес Si=28; молекулярный вес SiO2=60;
К примеру, содержание SiO2 в вес.% =70.4%.
70,4% – 60, где Х содержание Si в SiO2 в вес.%.
В приведенном расчете множитель 28/60 представляет собой частное от деления атомного веса определяемого элемента, в данном случае Si, на молекулярный вес окисла SiO2. Этот множитель остается постоянным применительно к любому значению содержания SiO2 в весовых %. Данная схема определения весовых количеств элемента с использованием атомных количеств применима к расчету содержаний любого элемента в весовых процентах по процентному содержанию его окисла. Поэтому нет необходимости в каждом конкретном случае составлять вышеприведенную пропорцию и решать ее. Следует принять отношение атомного веса элемента к его молекулярному весу за своего рода константу, расчетный коэффициент К, для использования при определении процентного содержания элементов по содержанию их окислов в весовых процентах. Определяем расчетный коэффициент К для каждого элемента по формуле, включающей в числители атомный вес элемента А, в знаменателе- молекулярный вес окисла:
Вычислить расчётные коэффициенты:
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
| K |
4. Результаты пересчетов выносим в таблицу 5.
| № пробы | Содержание в вес. % | ||||||||
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
5. Вычисляем дисперсию и стандартное отклонение
Дисперсия и стандартное отклонение позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним. Для выборки Х1, Х2, … Хn выборочная дисперсия (обозначаемая символом S 2 задается следующей формулой:
В общем случае выборочная дисперсия — это сумма квадратов разностей между элементами выборки и выборочным средним, деленная на величину, равную объему выборки минус один:
где X̅ — арифметическое среднее, n — объем выборки, Xi — i-й элемент выборки X.
Наиболее практичной и широко распространенной оценкой разброса данных является стандартное выборочное отклонение. Этот показатель обозначается символом S и равен квадратному корню из выборочной дисперсии:
| № пробы | Содержание в вес. % | ||||||||
| Si | Ti | Al | Fe 3+ | Fe 2+ | Mn | Mg | Ca | Na | K |
| 33,09 | |||||||||
| 29,78 | |||||||||
| 32,15 | |||||||||
| 28,41 | |||||||||
| 28,56 | |||||||||
 | 30,4 | ||||||||
| S 2 | 4,51 | ||||||||
| S | 2,12 |
Ни выборочная дисперсия, ни стандартное выборочное отклонение не могут быть отрицательными. Единственная ситуация, в которой показатели S 2 и S могут быть нулевыми, — если все элементы выборки равны между собой.
Дисперсия и стандартное отклонение позволяют оценить разброс данных вокруг среднего значения, иначе говоря, определить, сколько элементов выборки меньше среднего, а сколько — больше. Стандартное отклонение позволяет оценить величину колебаний элементов выборки вокруг среднего значения.
ГЕОХИМИЯ на ПРАКТИКЕ: 2) подготовка данных
Группа компаний ТЕЛЛУР
|
Решаем задачи геохимического картирования по вторичным ореолам рассеяния (лабораторная работа для студентов 3-го курса).
Этап 2: необходимо подготовить массив геохимических данных к работе — определить характер распределения каждого химического элемента, исключить аномальные значения.
Итак, мы вернулись с поля, нагруженные пробами почв. Сдали их в лабораторию, а взамен получили множество страниц с колонками чисел — содержаниями химических элементов в почвах. Теперь требуется очистить наши данные от мусора, чтобы затем приступить к поиску геохимических аномалий.
ЧТО МЫ ИМЕЕМ: таблицу данных по содержаниям химического элемента. Упростим ее до следующего вида:
столбец 1 — координата по широте («X» — для удобства берем не градусы, а прямоугольные координаты);
столбец 2 — координата по долготе («Y» — для удобства берем не градусы, а прямоугольные координаты);
столбец 3 — содержание химического элемента в пробе.
ПРИМЕЧАНИЕ: единицы измерения. Содержания химических элементов в горных породах, рудах и почвах измеряются в следующих единицах:
(а) массовый процент, мас.% (не надо называть его весовым, это безграмотно) — это единица для основных (т.н. породообразующих) элементов, их иногда называют «макроэлементами»;
(б) грамм на тонну, г/т — единица для измерения содержания «микроэлементов», которые содержатся в образце в малых количествах (ее придумали горняки, которым важно, сколько граммов металла содержится в тонне руды).
Коэффициент перехода между этими единицами — ДЕСЯТЬ ТЫСЯЧ. Т.е. 1 мас.% = 10000 г/т, а 1 г/т = 0,0001 мас.%. Никогда не путайте! Надо запомнить — «четыре ноля».
Иногда 1 г/т обозначают как 1 мг/кг (один миллиграмм на килограмм, эту единицу придумали лабораторщики, для которых объект — это малая навеска), еще реже — как 1 млн. -1 . Обратите внимание, почему.
Важный момент: в 1 тонне содержится 1 миллион грамм, т.е. 10 6 (именно поэтому 10 4 — это перевод между мас.% и г/т, т.к. 1% = 10 -2 ). Т.е. 1 грамм — это миллионная часть тонны. Поэтому зарубежом, где трава зеленее , нет, ароматнее , нет, не так, там, где нас нет , опять не так, где никто и двух слов по-русски связать не может, грамм на тонну называют «часть на миллион» (part per million) и обозначают ppm (произносится «пи-пи-эм», я же говорю Вам — смех и грех). При этом в названии единицы никак не звучит, что это не просто доля, а доля МАССОВАЯ. Это порой путает людей и приводит к ошибкам, потому что грамм на тонну — это всегда одна часть на миллион, но не всякая часть на миллион — это грамм на тонну.
В той же геохимии иногда расчеты ведутся в переводе на количества атомов. Тогда приходится использовать в качестве единиц атомный процент (ат.%) и «атом на миллион [атомов]» (англ. apm — atoms per million).
Можно еще вспомнить про метод ядерного магнитного резонанса (ЯМР-спектроскопия), где спектральная шкала измеряется в миллионных долях (ppm), т.е. тоже в частях на миллион, но уже тем более не массовых (и даже не атомных). И я уж совсем молчу про малышку на миллион (может, она должна называться baby per million. ). Все, хватит примечания, возвращаемся к теме.
ЧТО НАМ ПОНАДОБИТСЯ: для начала — электронная таблица, например Microsoft Excel (не забудьте приобрести лицензионную версию!) или Apache OpenOffice Calc (он бесплатный). А, поскольку считать мы будет статистические параметры, в дополнение к электронным таблицам используем специальное ПО для математической статистики: программу STATISTICA фирмы StatSoft (в ВУЗы продается со скидкой!). Почему именно это ПО, а не конкурентов? А вот люблю эту прогу, очень она мощная и удобная, все умеет и понятно показывает. Жалко, что любовь не купишь, так бы я ее конвертировал в пожизненную лицензию от StatSoft!
ОФИЦИАЛЬНЫЕ СТРАНИЦЫ производителей ПО:
ОБЪЯСНЕНИЕ 1. Работа с электронной таблицей. В процессе работы нам придется выполнять стандартные операции в электронной таблице: использовать формулы, которые будут ссылаться на ячейки и их диапазоны и пр. Читатели данного руководства должны уметь выполнять такого рода действия. Сослаться на ячейку таблицы или на диапазон ячеек можно, набрав в строке формулы соответствующие адреса ячеек или ткнув в ячейки мышкой. Как конкретно это делается, я объяснять не буду. Если читатель не умеет — пусть сначала научится базовым приемам работы в электронной таблице. Эти приемы одинаковы для всех таблиц.
ОБЪЯСНЕНИЕ 2. Версии программ. Конкретные меню программ и возможности команд порой меняются от версии к версии. Я использую здесь меню MS Office 2003 и OpenOffice 3.2. Почему этих версий? А потому. Если у Вас другая версия, и меню выглядит иначе, — заходим в интернет и ищем нужную нам функцию или команду на справочных сайтах, с помощью поисковиков. Если знать, как выглядит функция в одной версии, нетрудно найти ее в другой, тем паче, что интернет кишит паническими криками о помощи людей, попавших именно в такую ситуацию. Делать сравнение разных версий я не буду.
Согласны? Тогда едем дальше.
§2. Замена нолей: «нолей в природе не бывает» (логарифм, коэффициент вариации и мн. др.). Геохимический и лабораторно-аналитический подход. Загадочный «предел обнаружения».
§7. Проверка дисперсии по-ленински: переменная должна быть переменной!
§8. Как составить отчет к первой части лабораторной работы.




